Ordinary Differential Equations

1. Series Reactions

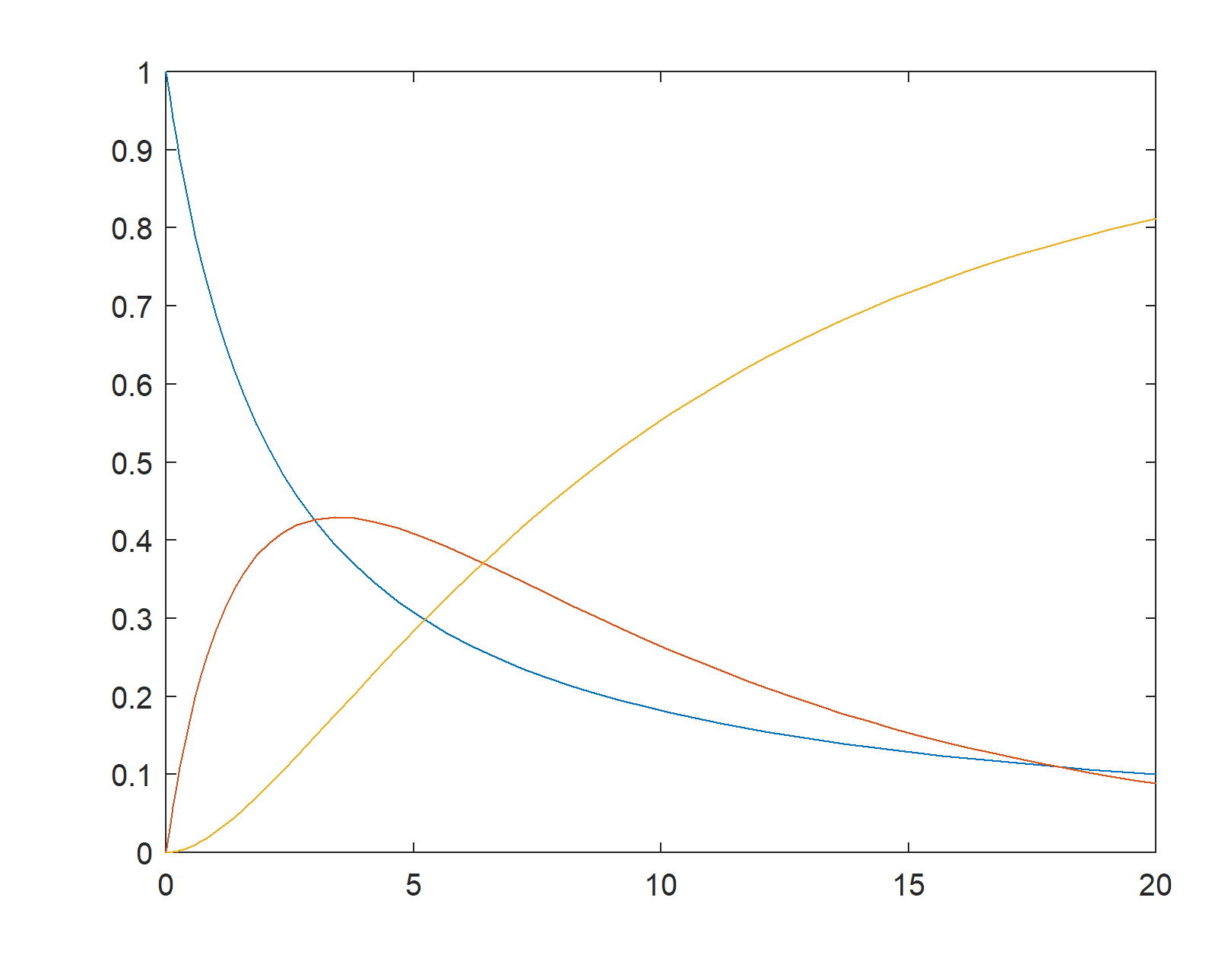
The concentration change as a function of time for the series reaction \[ A \stackrel{k_1}{\rightarrow} B \stackrel{k_2}{\rightarrow} C \]
is given below:
\[ \begin{align*}\frac{dC_A}{dt} &= -k_1C_A^{n_1} \\
\frac{dC_B}{dt} &= k_1C_A^{n_1} - k_2C_B^{n_2} \\
\frac{dC_C}{dt} &= k_2C_B^{n_2}\end{align*}\]

The given differential equations are solved by Runge-Kutta method as below:

% ConcTime_BatchReactor.m
% Done on 27-Feb-2012
% Updated on 15-June-2022
% Subramanian M
% solutions to rate equations
% to get C vs t for series reactions A -> B -> C
% Rice - Applied Mathematics and Modeling for Chemical Engineers

clear; close all; clc;
k = [0.45 0.16];
n = [2 1];  % The order of A->B and B->C 

% [TOUT,YOUT] = ODE45(ODEFUN,TSPAN,Y0,OPTIONS, PARAMETERS)
[t, C] = ode45(@BatchReactorEqns, [0 20], [1 0 0], [], k, n);

plot(t, C)

function Cdot = BatchReactorEqns(~, C, k, n)
% To solve 
% dC1/dt = -k1*C1^n1
% dC2/dt = k1*C1^n1-k2*C2^n2
% dC3/dt = k2*C2^n2
% CA0 = 1; CB0 = 0; CC0 = 0;
Cdot = zeros(3,1);  % a column vector
Cdot(1) = -k(1)*C(1)^n(1);
Cdot(2) = k(1)*C(1)^n(1)-k(2)*C(2)^n(2);
Cdot(3) = k(2)*C(2)^n(2);
end

>> ConcTime_BatchReactor