Unit-2: Thermodynamic Properties of Real Gases
| Site: | MSubbu Academy |
| Course: | Thermodynamics - Free Course |
| Book: | Unit-2: Thermodynamic Properties of Real Gases |
| Printed by: | Guest user |
| Date: | Saturday, 26 April 2025, 11:39 AM |
Table of contents
- Contents
- T-v diagram for the heating process of water at constant pressure
- T-v diagram of contant-pressure phase-change processes
- PVT Diagram of Pure Components
- PT Diagram
- PT Diagram of Water
- PV Diagram
- PV Diagram of Water
- TV Diagram of Water
- Ideal Gas Equation
- van der Waals Equation
- van der Waals Equation
- van der Waals Constants
- Comparison of ideal and van der Waals gas
- Redlich-Kwong Equation
- Peng-Robinson Equation
- Berthelot Equation
- Dieterici Equation
- Example: Trial and Error solution of cubic Equation
- Derivation for a and b of van der Waals
- Example : van der Waals equation - Derivation for a and b in another way van der Waals equation is given as
- Dieterici Equation
- Compressibility Factor
- Virial Equation
- Corresponding State Principle
- Equation of State for a Single Phase
- Equation of State for Liquids
- Quality of Vapor (Dryness Fraction)
- Steam Tables
- Single-phase tables
- Example - Volume from Steam Tables
- Integration Calculations
- Surprise Test
Contents
PVT behaviour of fluids; Mathematical representation of PVT behaviour; Generalized compressibility factor correlation; Generalized equations of state.
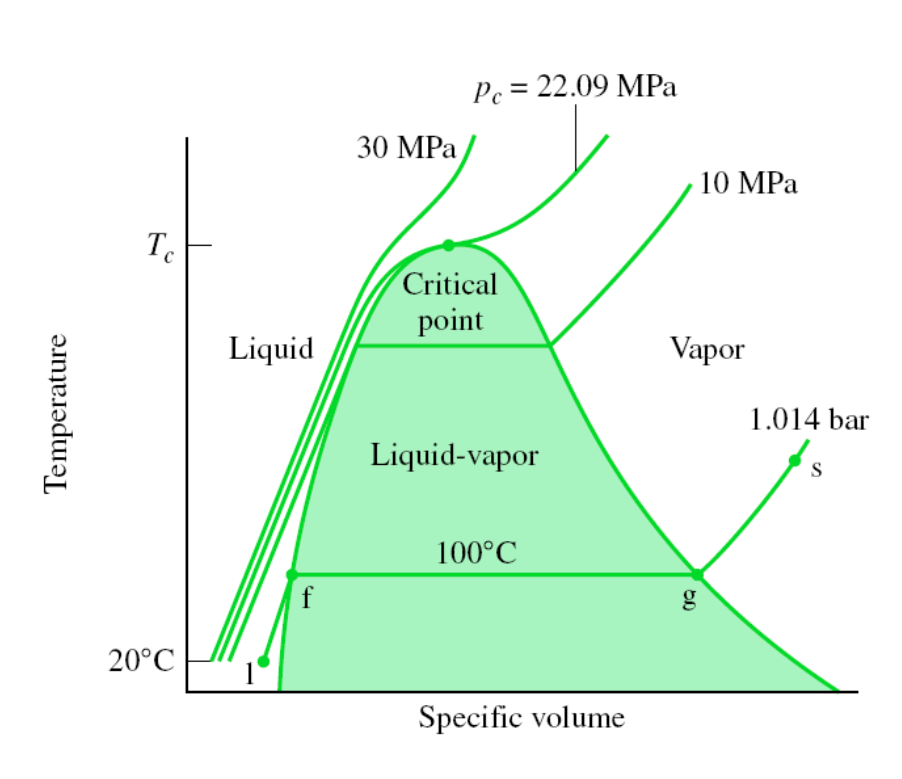
T-v diagram for the heating process of water at constant pressure
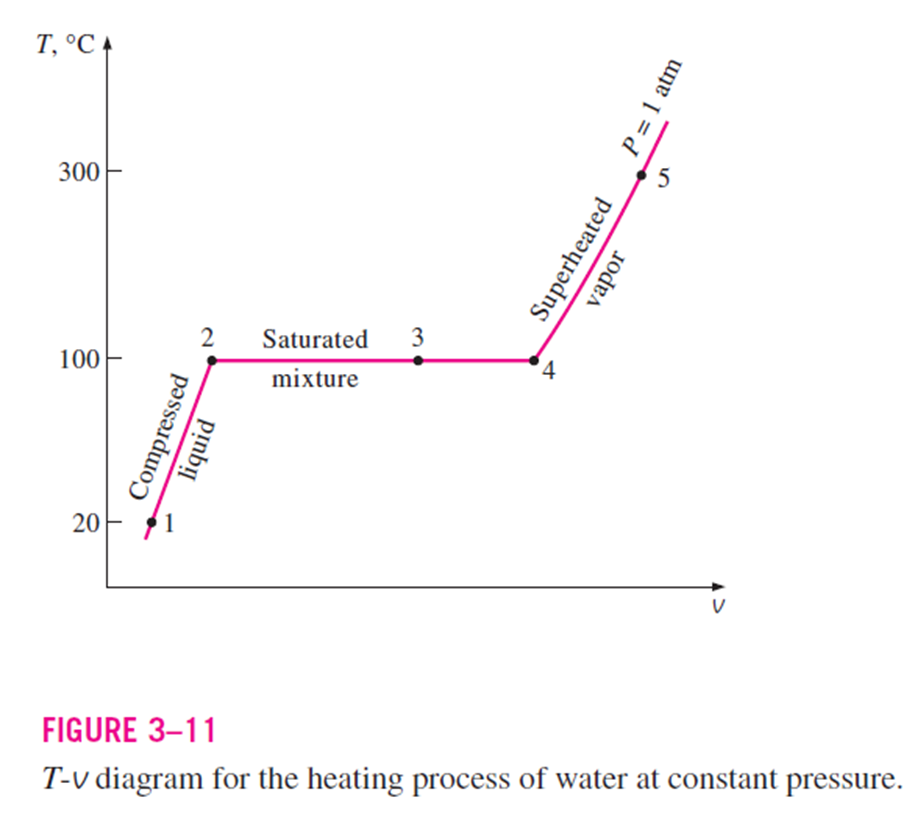

T-v diagram of contant-pressure phase-change processes



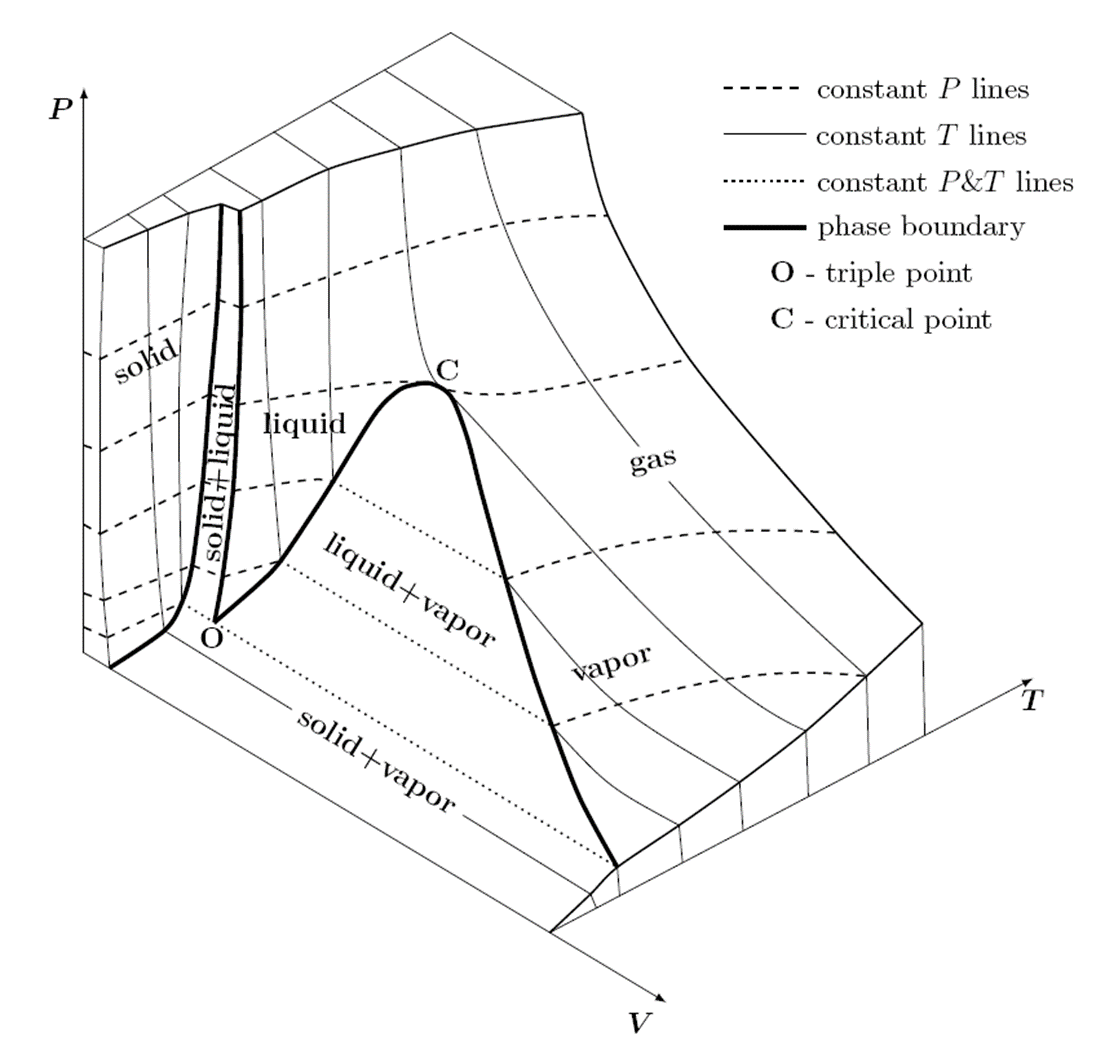
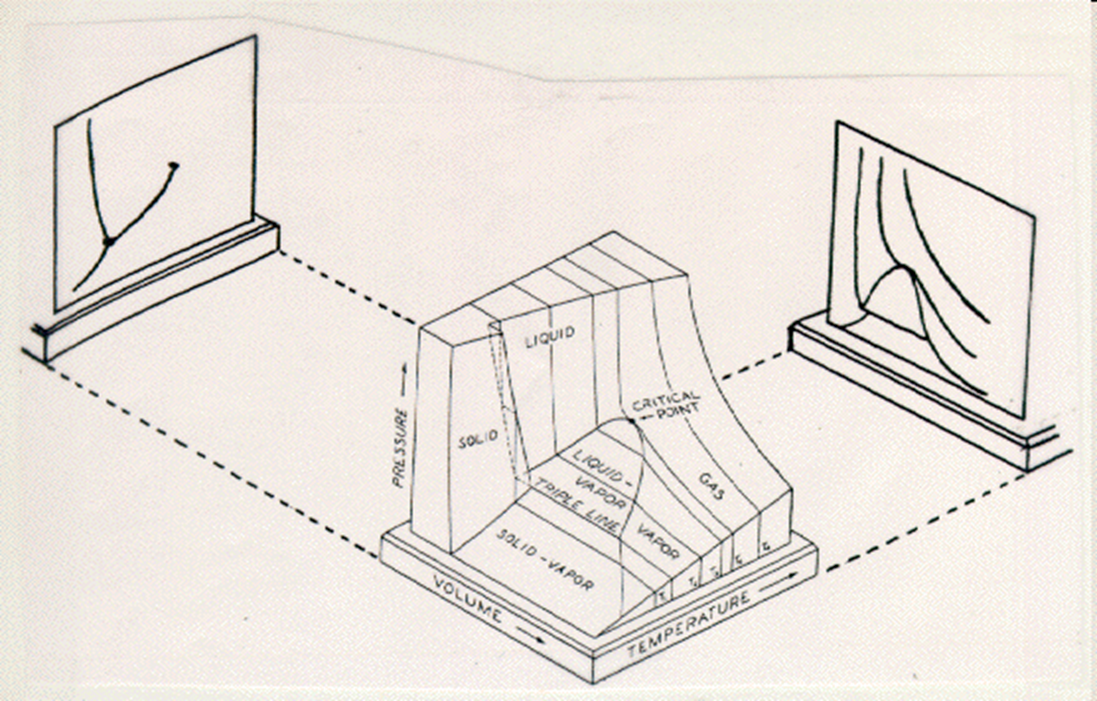
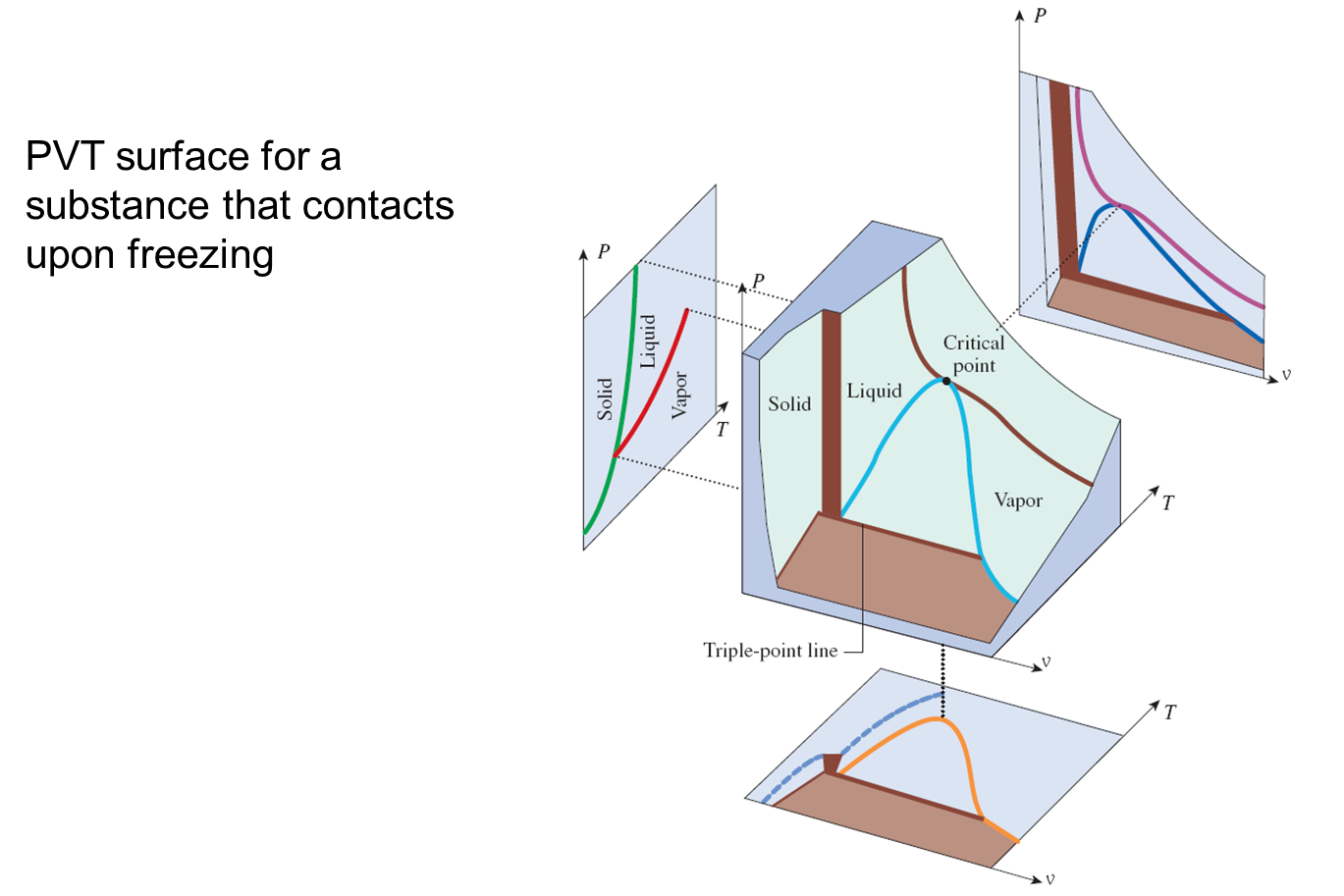
PVT Diagram of Pure Components
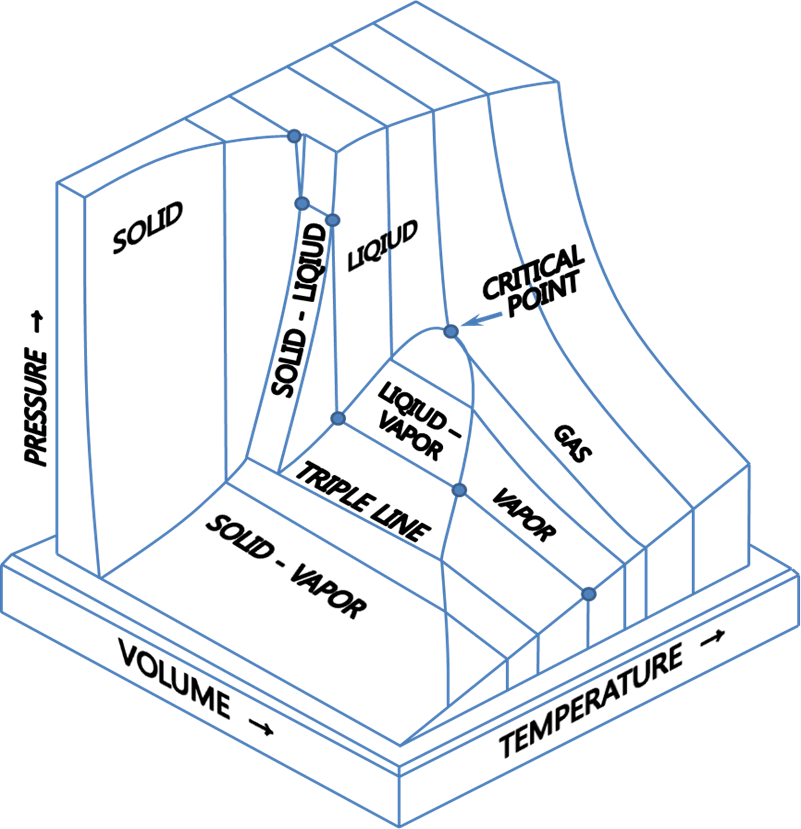

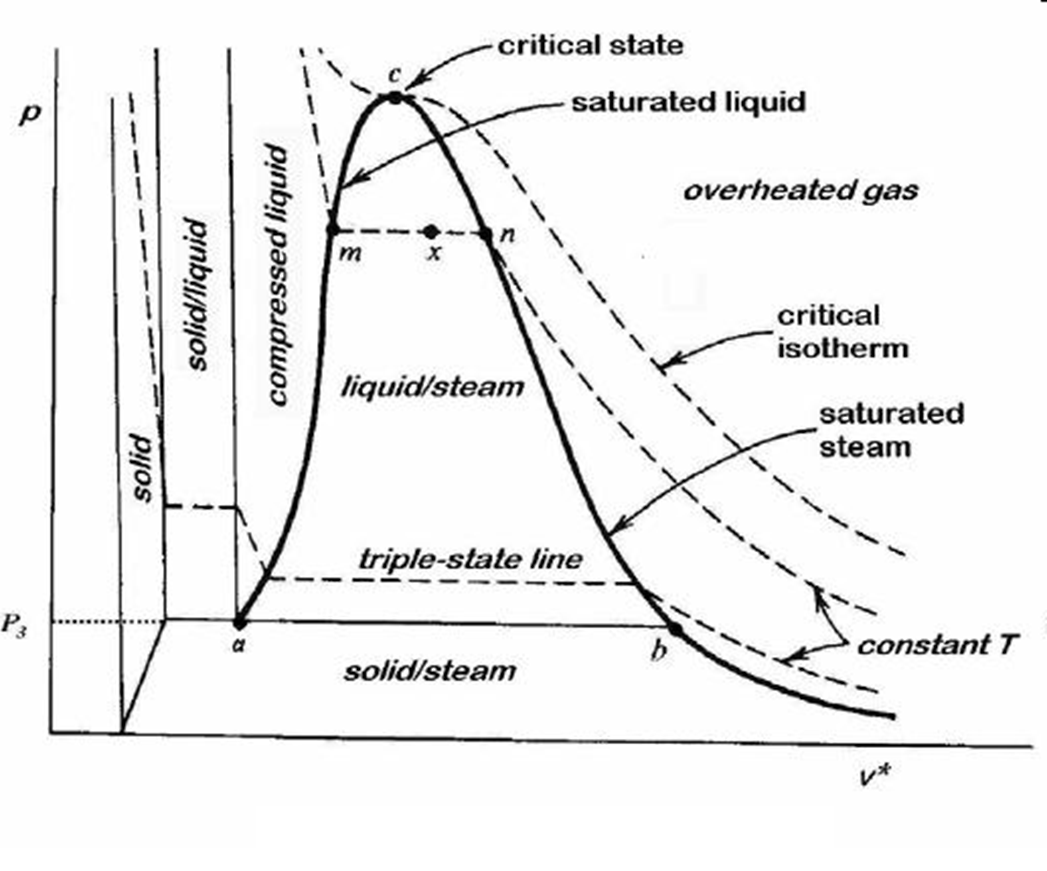
The PVT surface above represents a substance which contracts upon freezing. Most substances do so, the notable exception being water, bismuth and antimony which expands upon freezing. The expansion of water upon freezing has an enormous impact on the nature of the Earth.
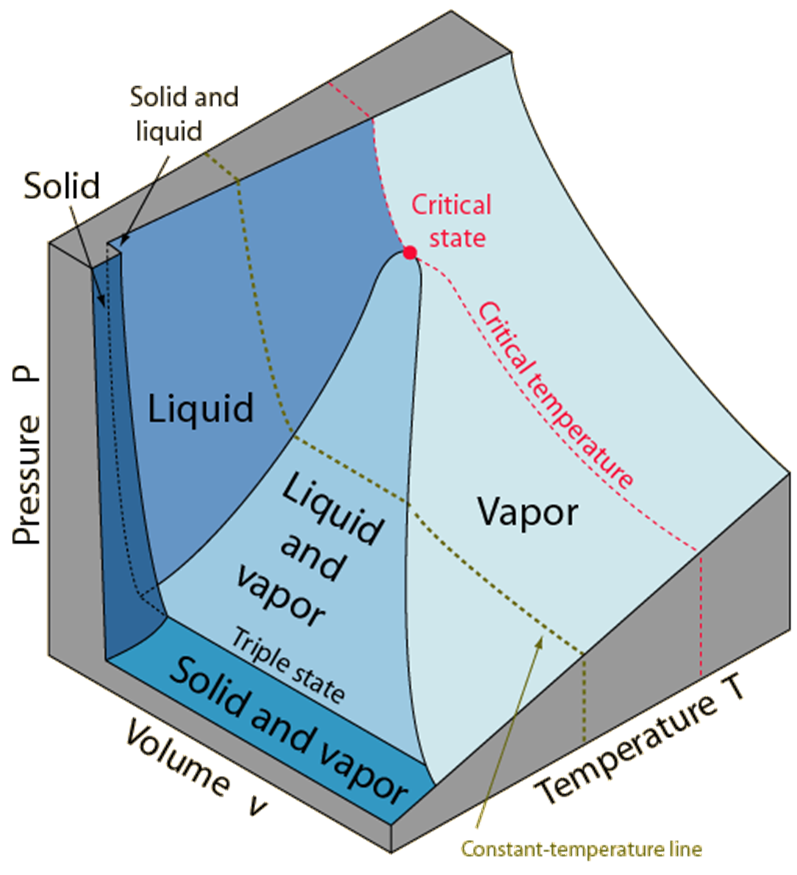
PT Diagram
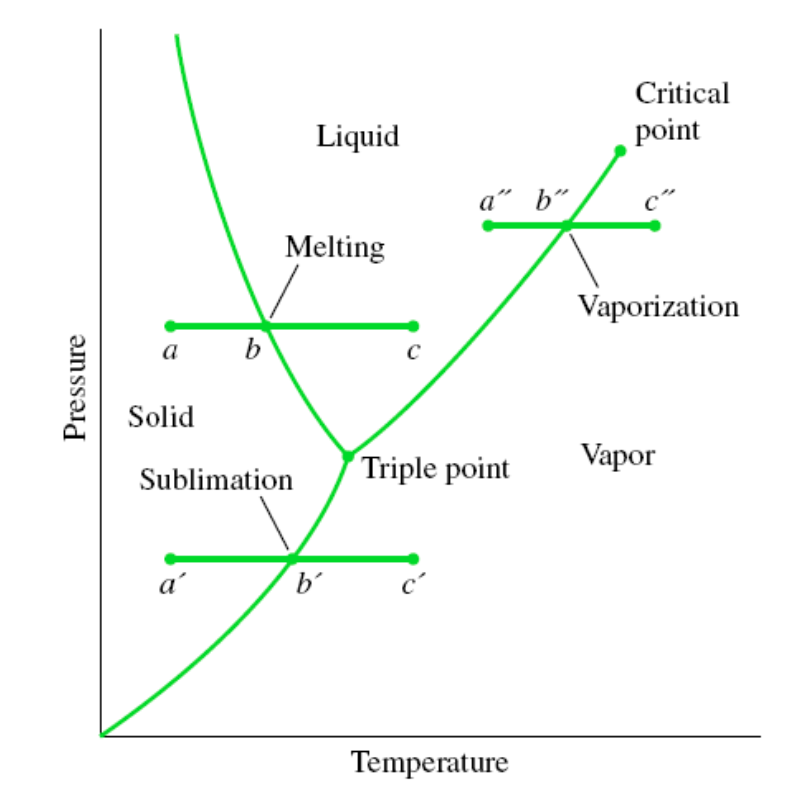
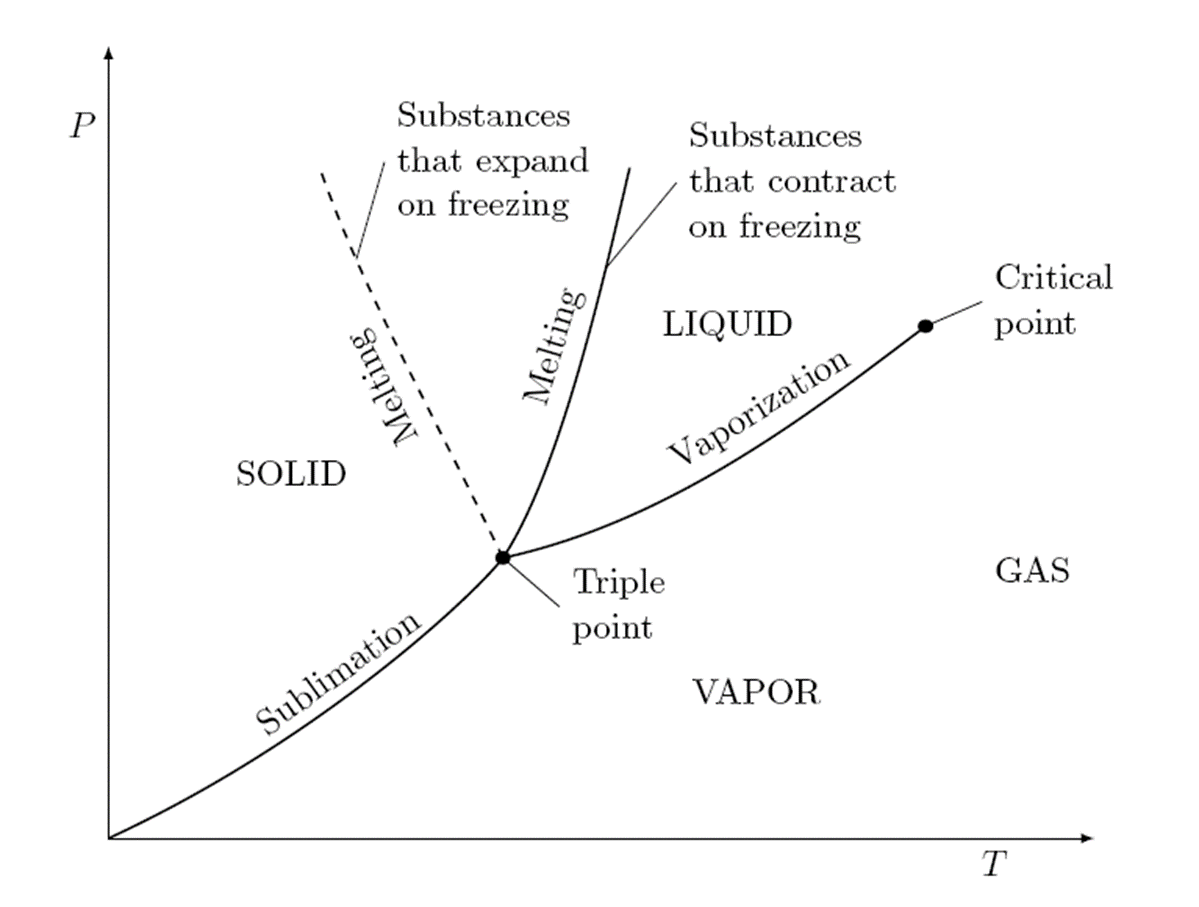
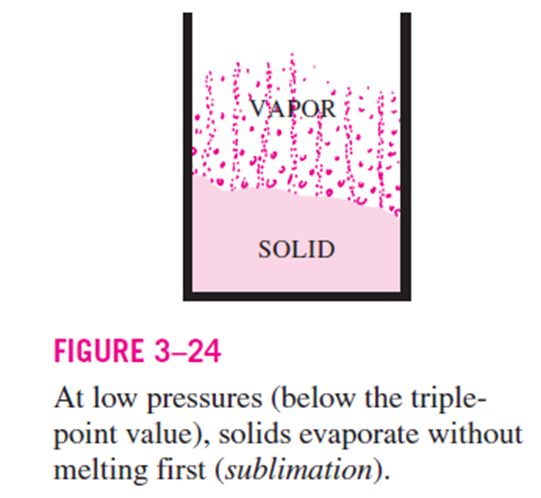
Passing from the solid phase directly into the vapor phase is called sublimation.
For substances that have a triple-point pressure above the atmospheric pressure such as solid CO2 (dry ice), sublimation
is the only way to change from the solid to vapor phase at atmospheric conditions.
PT Diagram of Water
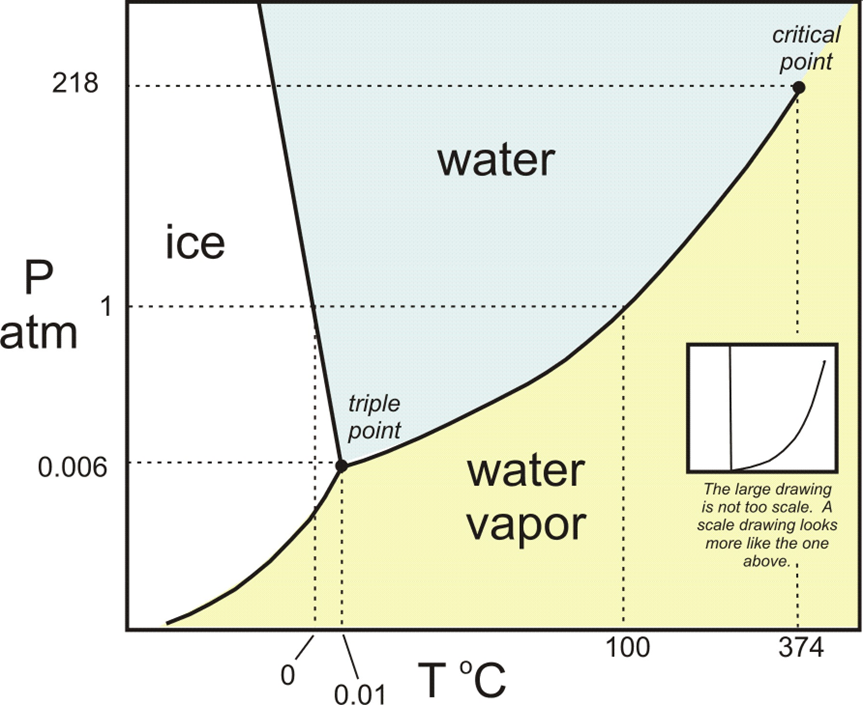
Triple
point: P = 611.7 N/m2; T =
0.01oC
Critical point: P= 220.64 x 105 N/m2; T = 374oC
Normal boiling point: 100oC; Normal freezing point: 0oC (1 atm)
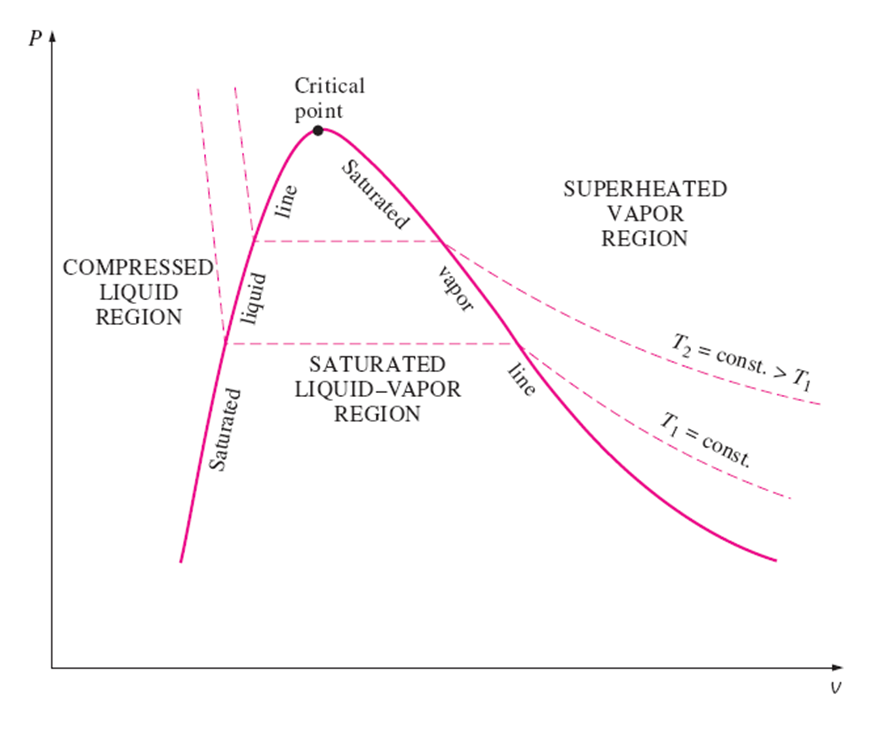
PV Diagram


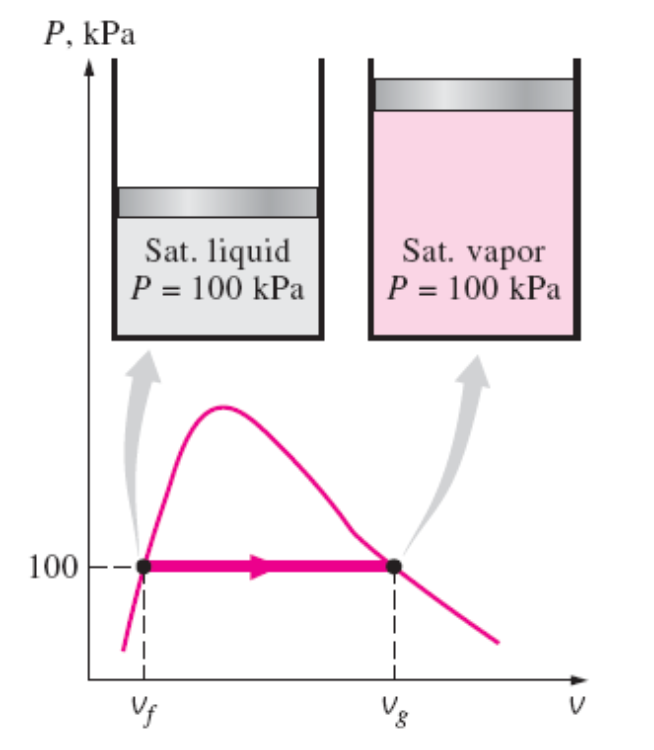
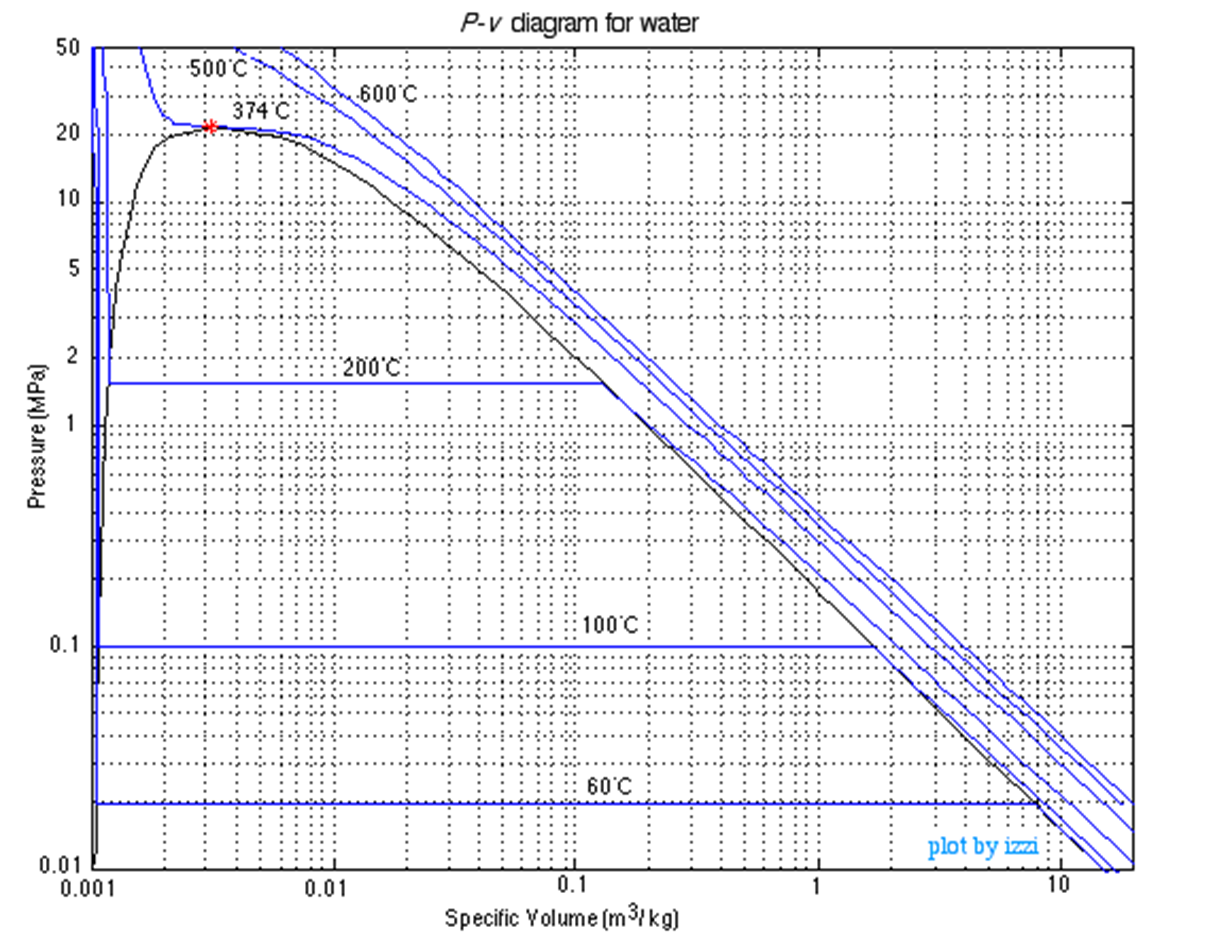
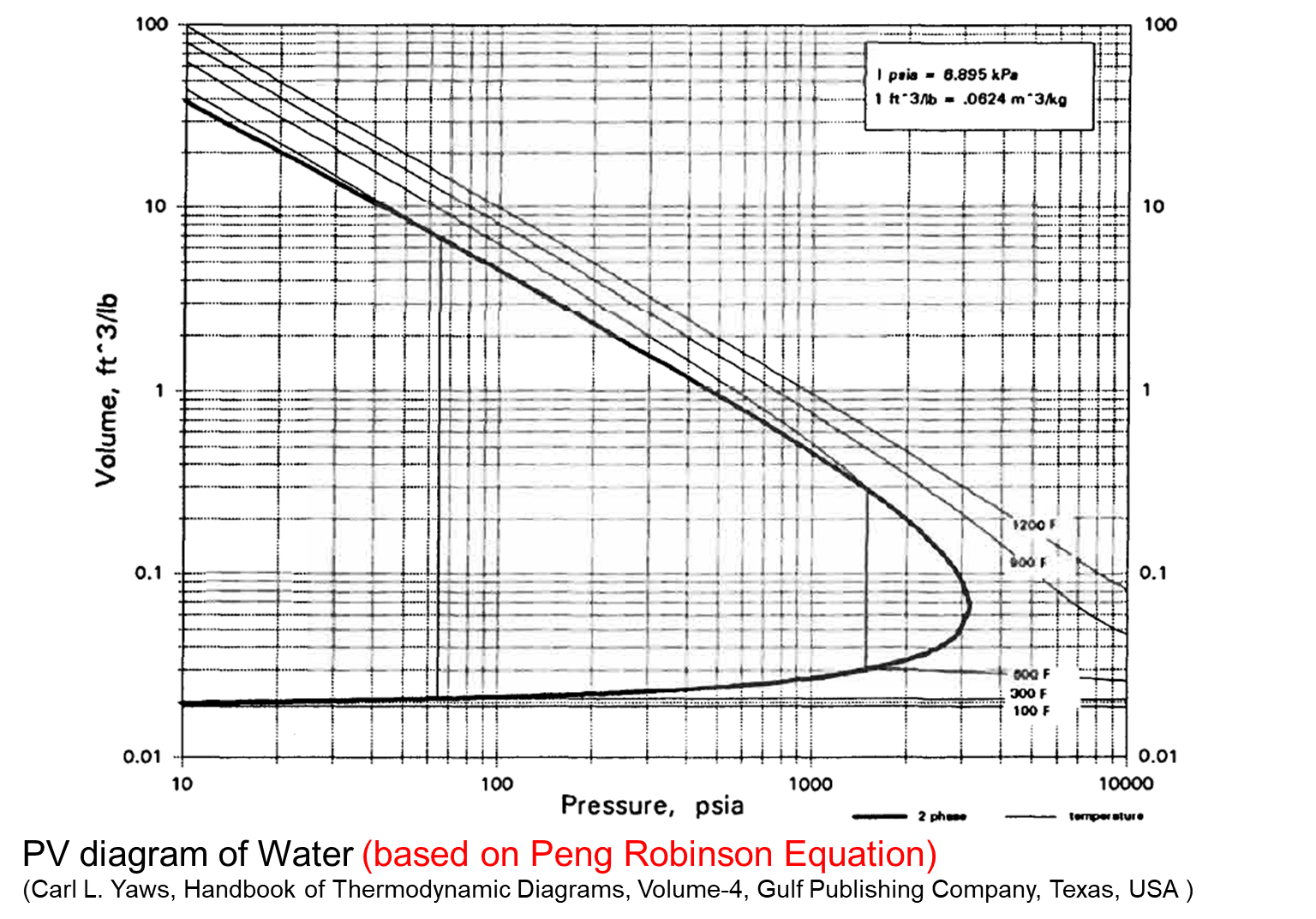
PV Diagram of Water

TV Diagram of Water




Ideal Gas Equation

![]()


van der Waals Equation


van der Waals Equation

- The parameter b is related to the size of each molecule. The volume that the molecules have to move around in is not just the volume of the container V, but is reduced to ( V - b )
- The parameter a is related to intermolecular attractive force between the molecules, and 1/V is the density of molecules. The net effect of the intermolecular attractive force is to reduce the pressure for a given volume and temperature.
- When the density of the gas is low (i.e., when 1/V is small and b is small compared to V) the van der Waals equation reduces to that of the ideal gas law.
van der Waals Constants
|
Substance |
a (J. m3/mole2) |
b (m3/mole) |
Pc (MPa) |
Tc (K) |
|
Air |
1.1358 |
3.64x10-5 |
3.77 |
133 |
|
Carbon Dioxide (CO2) |
1.3643 |
4.27x10-5 |
7.39 |
304.2 |
|
Nitrogen (N2) |
1.1361 |
3.85x10-5 |
3.39 |
126.2 |
|
Hydrogen (H2) |
1.0247 |
2.65x10-5 |
1.30 |
33.2 |
|
Water (H2O) |
1.5507 |
3.04x10-5 |
22.09 |
647.3 |
|
Ammonia (NH3) |
1.4233 |
3.73x10-5 |
11.28 |
406 |
|
Helium (He) |
1.00341 |
2.34x10-5 |
0.23 |
5.2 |
|
Freon (CCl2F2) |
1.0780 |
9.98x10-5 |
4.12 |
385 |
Observe that inert gases like Helium have a low value of a as one would expect since such gases do not interact very strongly, and that large molecules like Freon have large values of b.
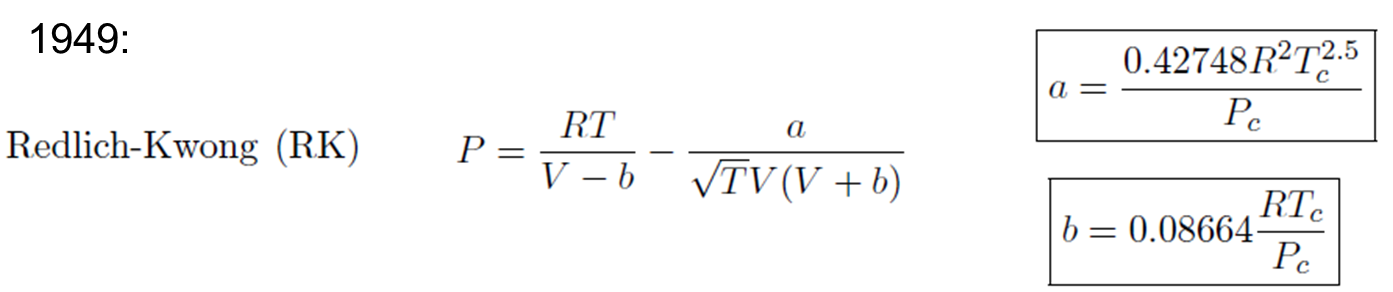
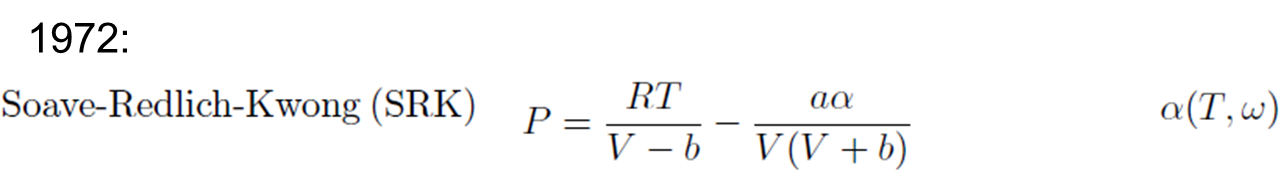
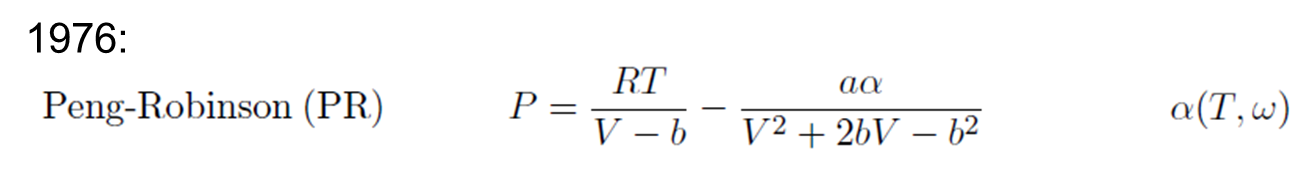
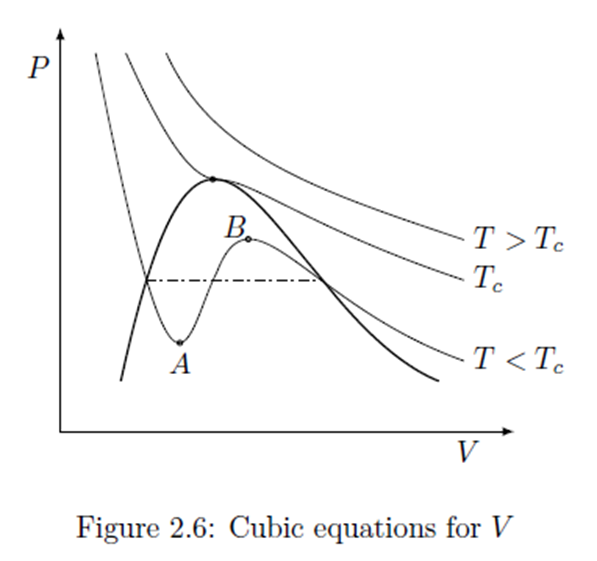
Comparison of ideal and van der Waals gas



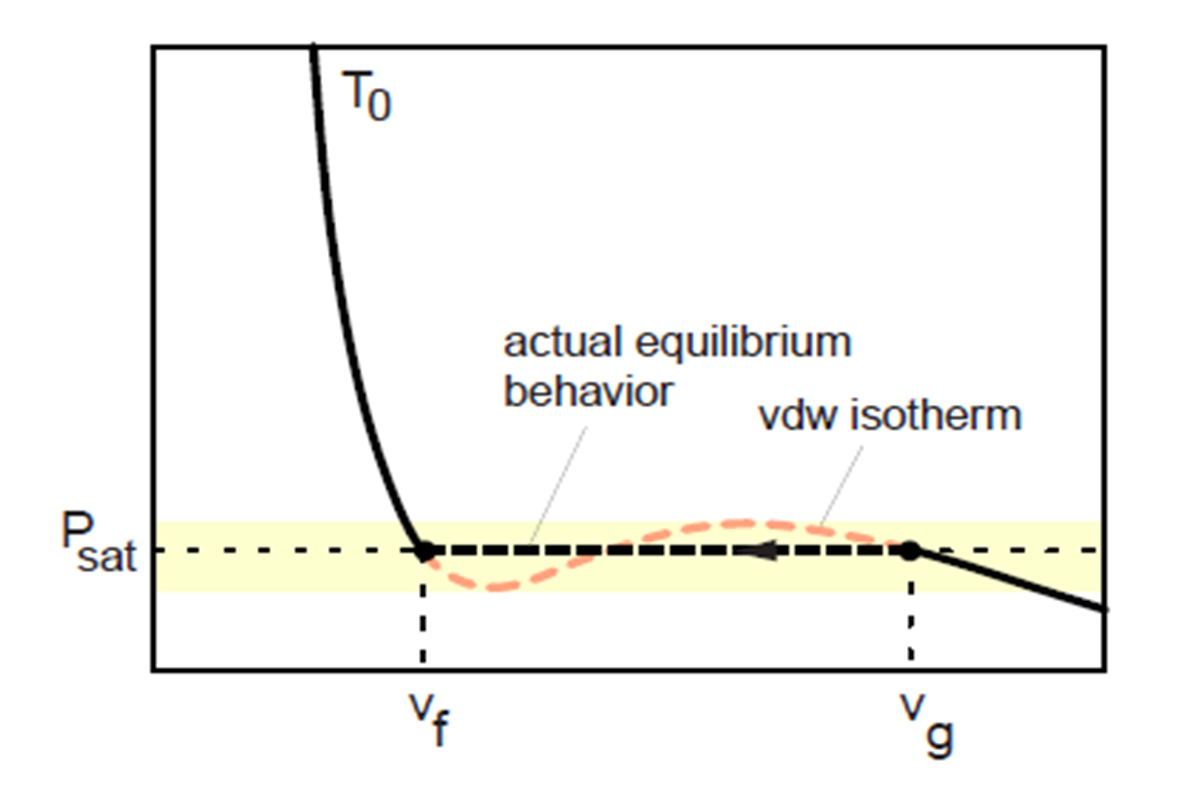
Comparison of actual behavior during isothermal compression to prediction of van der Waals equation.
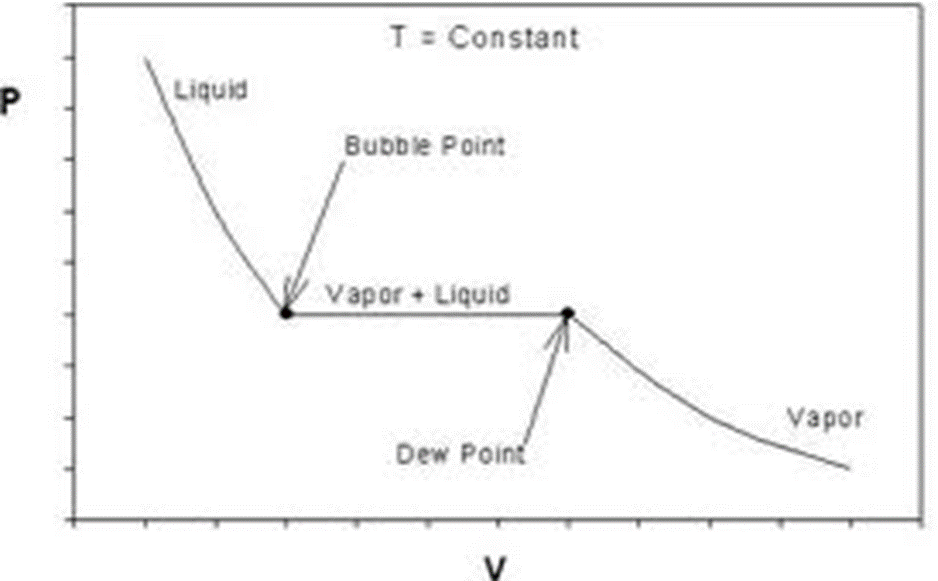
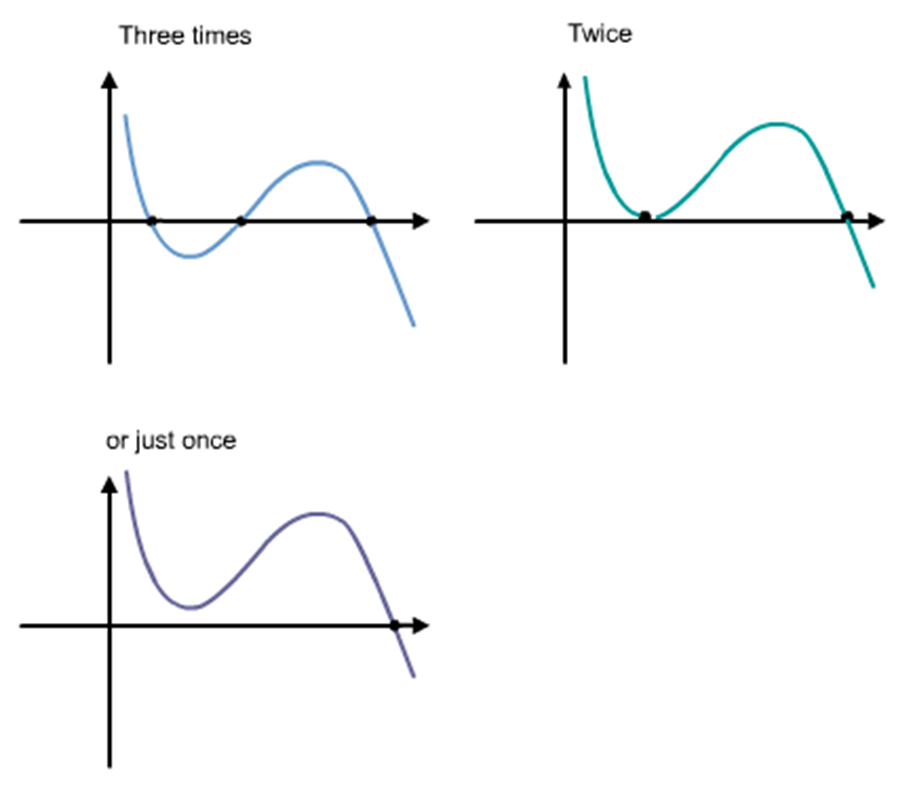
An
isotherm of the van der Waals equation for T < Tc.
Redlich-Kwong Equation
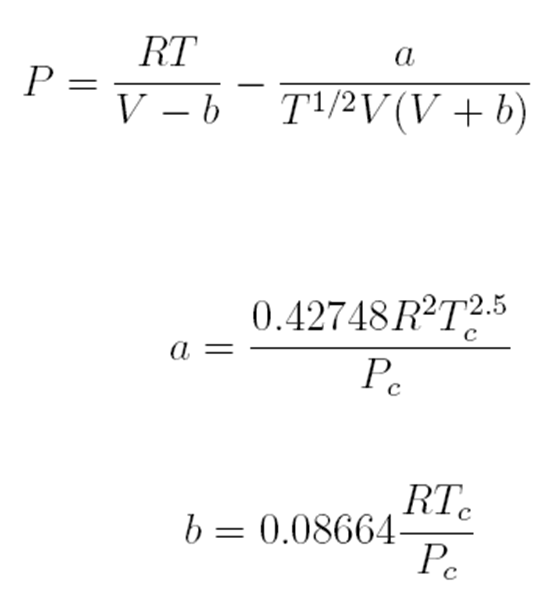
Peng-Robinson Equation

Berthelot Equation

Dieterici Equation
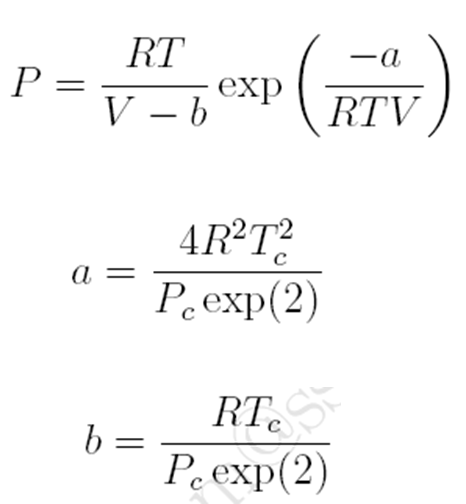
Example: Trial and Error solution of cubic Equation



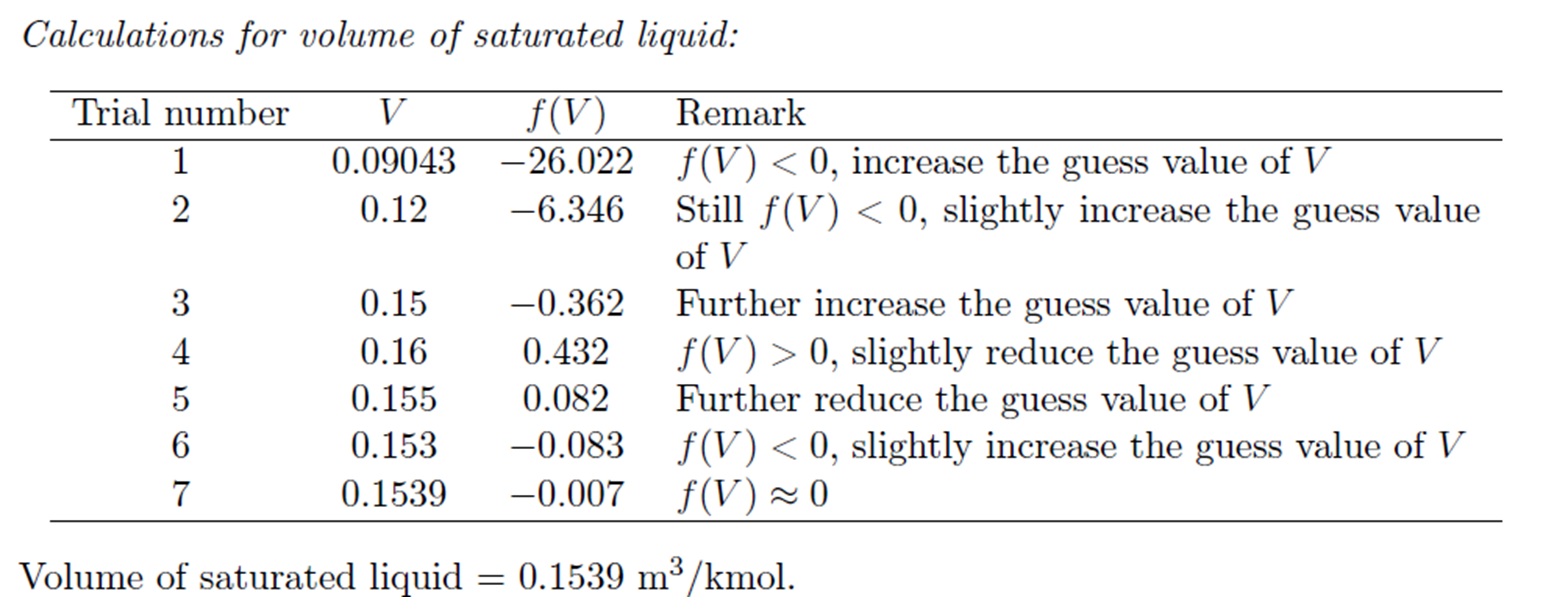



Derivation for a and b of van der Waals



Example : van der Waals equation - Derivation for a and b in another way van der Waals equation is given as


Dieterici Equation






Compressibility Factor

Virial Equation
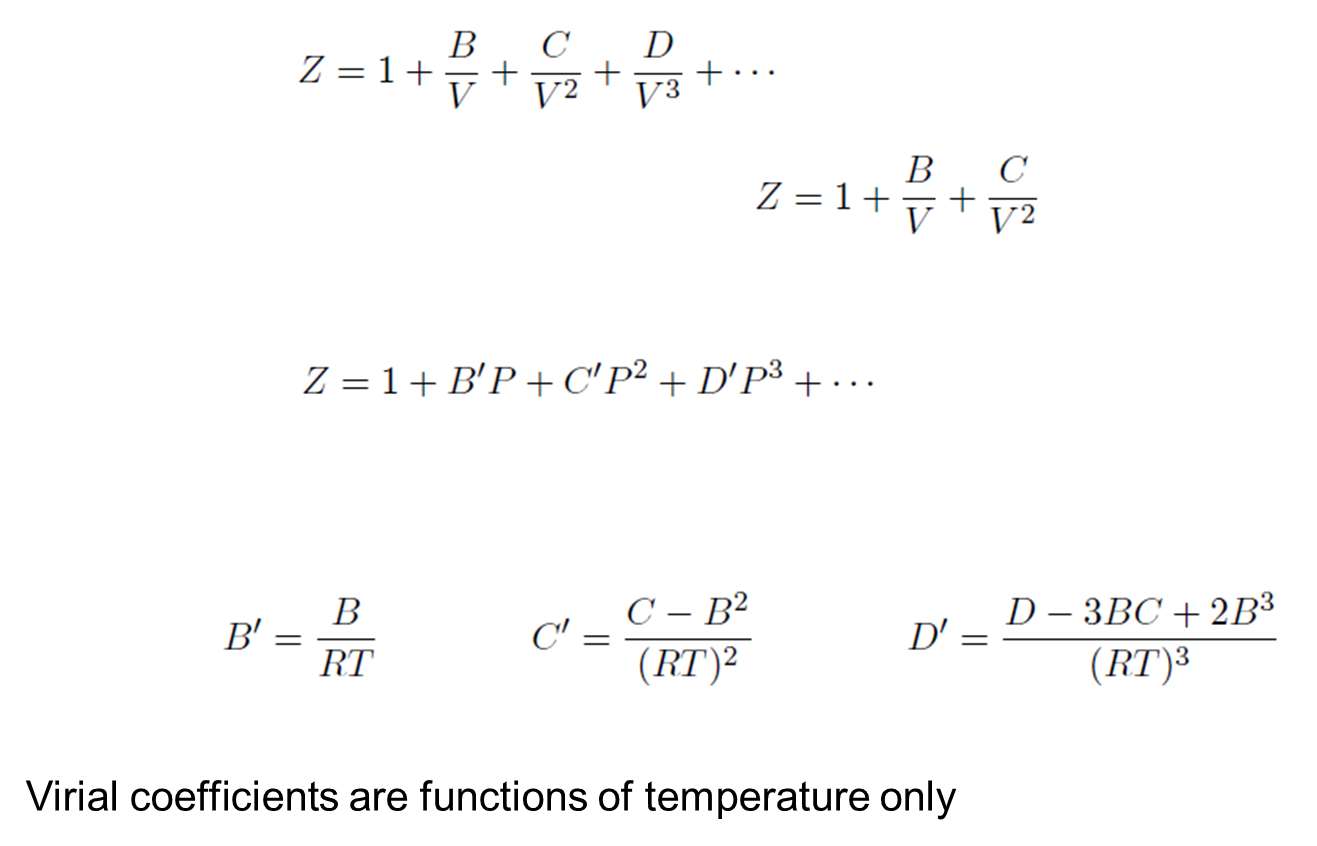
Corresponding State Principle




Equation of State for a Single Phase


Equation of State for Liquids

Quality of Vapor (Dryness Fraction)


Steam Tables

Single-phase tables






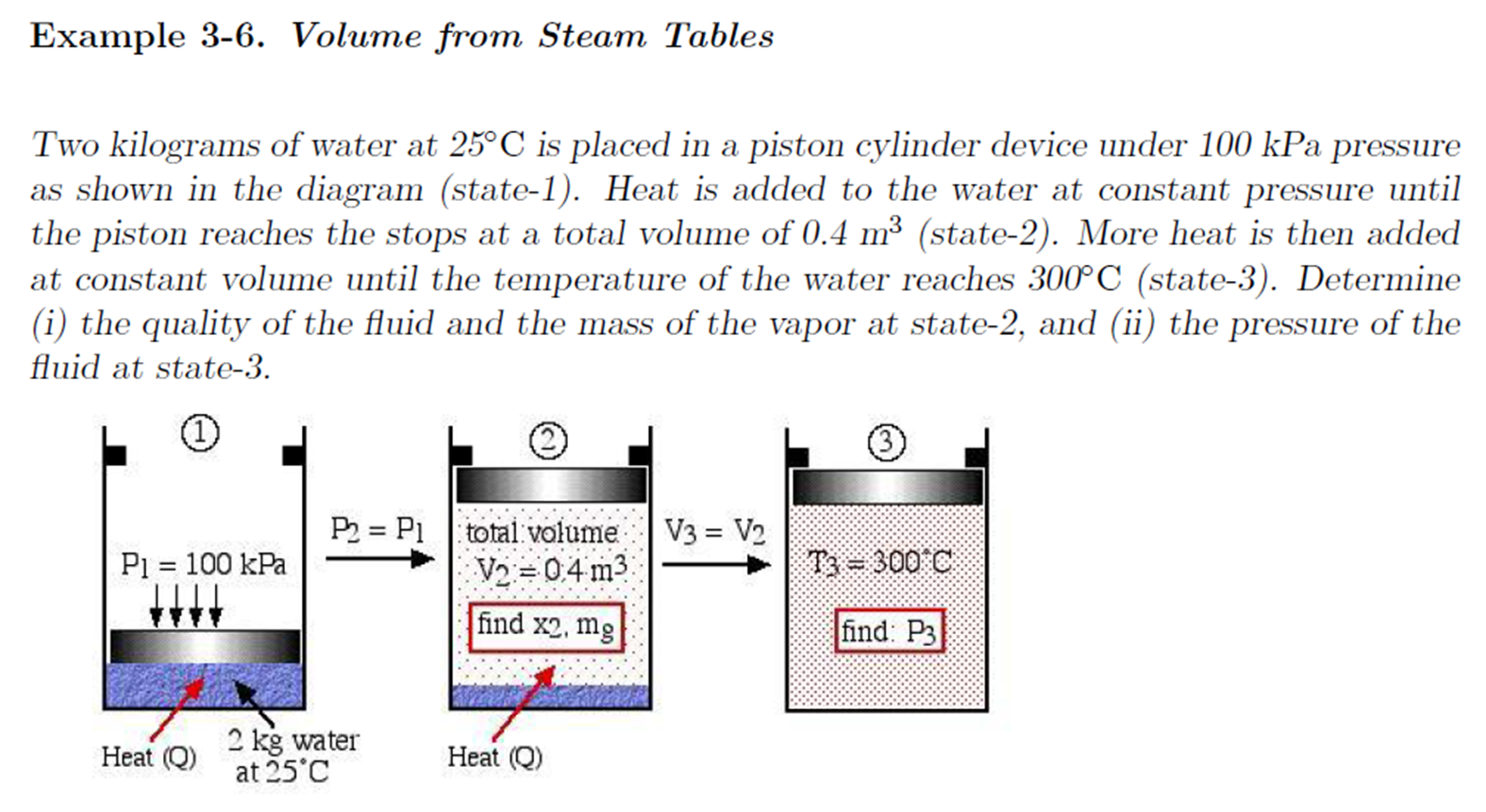
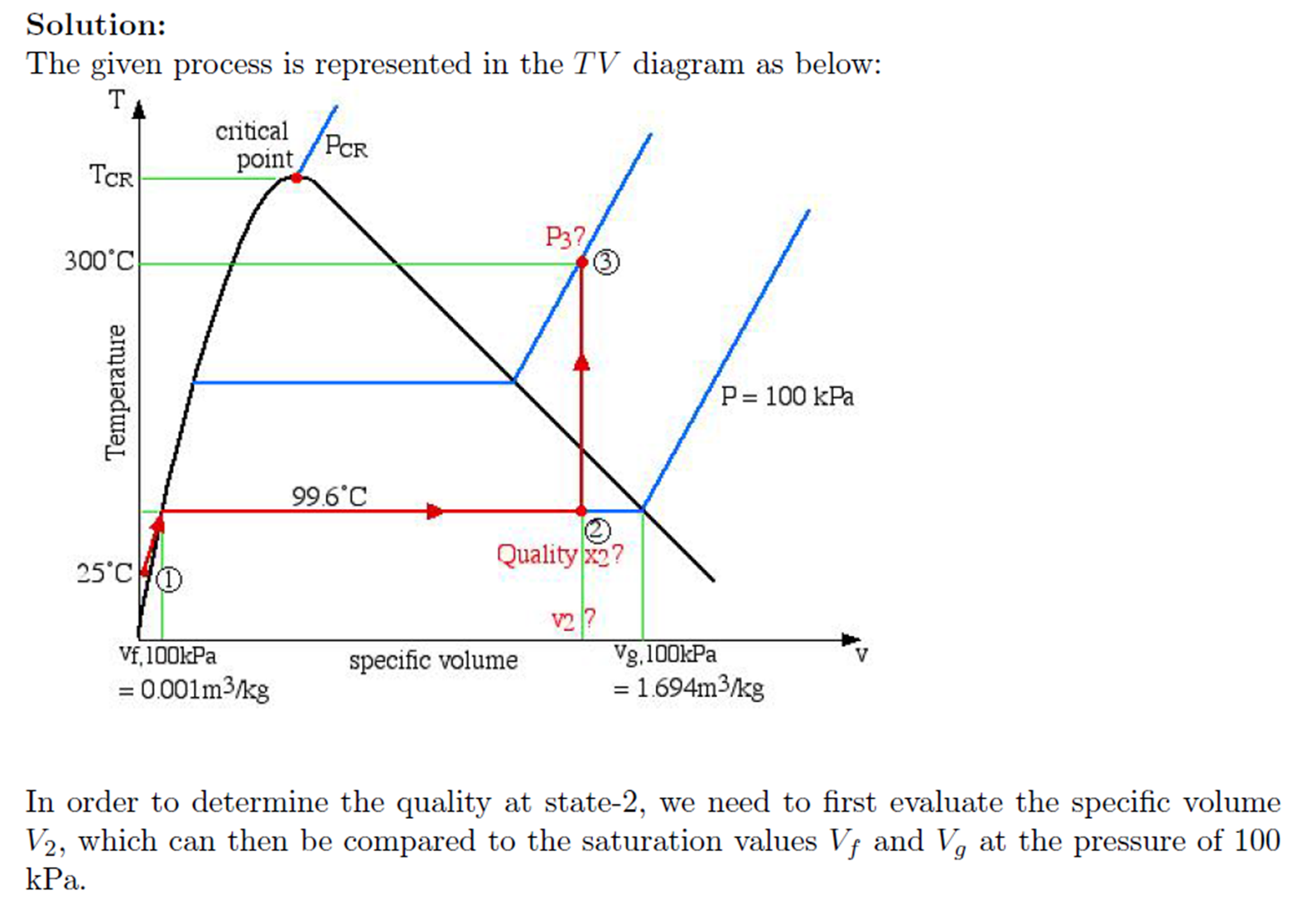
Example - Volume from Steam Tables


From the corresponding state principle by
considering Z as a
function of (Tr, Pr)
estimate the volume of 1 kmol of
oxygen at 200 K and 6 x 106
N/m2. (Pc
= 5.05 x 106 N/m2; Tc =
155 K). Z
values for various Tr, Pr are
as given below:
|
Z |
||||
|
Tr \( \downarrow \)Pr \( \rightarrow \) | 0.8 |
1.0 |
1.2 |
1.5 |
|
1.1 |
0.7649 |
0.6880 |
0.5984 |
0.4580 |
|
1.2 |
0.8330 |
0.7858 |
0.7363 |
0.6605 |
|
1.3 |
0.8764 |
0.8438 |
0.8111 |
0.7624 |
|
1.4 |
0.9062 |
0.8827 |
0.8595 |
0.8256 |
|
1.5 |
0.9278 |
0.9103 |
0.8933 |
0.8689 |
First by considering the interpolation at fixed values of Pr, get Z; then at fixed Tr value get the Z.
That way, you will get Z as 0.807
Integration Calculations


Surprise Test