2-Conduction - One Dimensional Heat Conduction Equation
3. One Dimensional Heat Conduction Equation
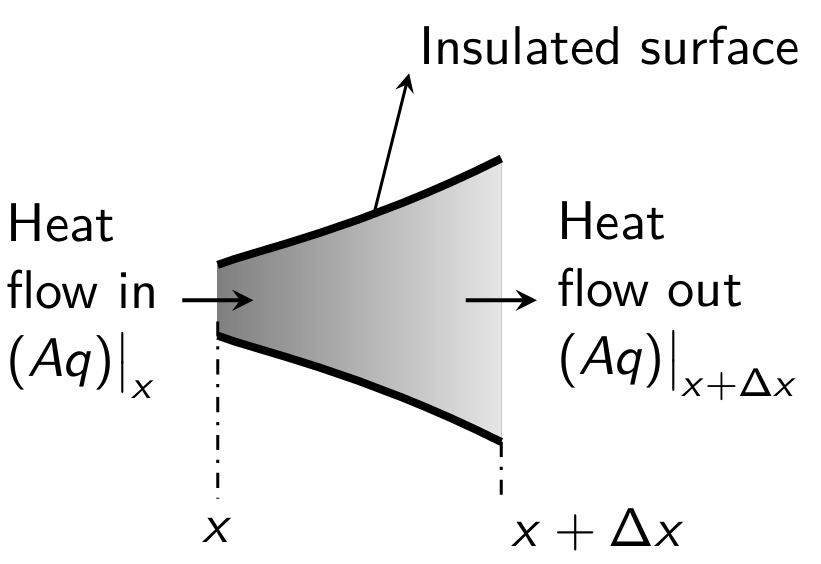
Let us consider a volume element of thickness \(\Delta x\) and having an area \(A\) normal to the coordinate axis \(x\), as shown in the figure. The energy balance equation for this volume element is given by: \[\underset{\text{I}}{\left(\begin{array}{c}\text{Net rate of} \\ \text{heat gain by} \\ \text{conduction} \end{array}\right)} + \underset{\text{II}}{\left(\begin{array}{c}\text{rate of} \\ \text{energy} \\ \text{generation} \end{array}\right)} = \underset{\text{III}}{\left(\begin{array}{c}\text{rate of} \\ \text{increase of} \\ \text{internal energy} \end{array}\right)} \tag*{(1)}\]
The net rate of heat gain by the element by conduction is given by \[\text{I} = (Aq)\big|_{x} - (Aq)\big|_{x+\Delta x}\]
The rate of energy generation in the element having a volume \(A\Delta x\) is given by \[\text{II} = A\Delta x \dot{g}\] where \(\dot{g}=\dot{g}(x,t)\) is the rate of energy generation per unit volume.
The rate of increase of internal energy of the internal energy of the volume element resulting from the change of temperature with unit time is given by \[\text{III} = A\Delta x \,\rho C_P\frac{\partial T(x,t)}{\partial t}\] (Note: Internal energy change is \(mC_V\Delta T\); but for liquids and solids, \(C_P\approx C_V\)).
Substituting for the quantities in Eqn.(1), and rearranging, we get \[-\frac{1}{A}\frac{\left((Aq)\big|_{x+\Delta x} - (Aq)\big|_{x}\right)}{\Delta x} + \dot{g} = \rho C_P\frac{\partial T(x,t)}{\partial t}\] As \(\Delta x \rightarrow 0\), \[\frac{\left((Aq)\big|_{x+\Delta x} - (Aq)\big|_{x}\right)}{\Delta x} = \frac{\partial}{\partial x}(Aq) \qquad \left(\begin{array}{c} \text{{from the definition}} \\ \text{{of derivative}} \end{array}\right)\] And, \(\displaystyle q=-k\frac{\partial T}{\partial x}\). Therefore, the above equation becomes \[{\frac{1}{A} \frac{\partial}{\partial x}\left(Ak\frac{\partial T}{\partial x}\right) + \dot{g} = \rho C_P\frac{\partial T(x,t)}{\partial t} \tag*{(2)} }\] This is the general equation for one dimensional heat conduction.
