6. One Dimensional Steady State Heat Conduction through Flat Plate





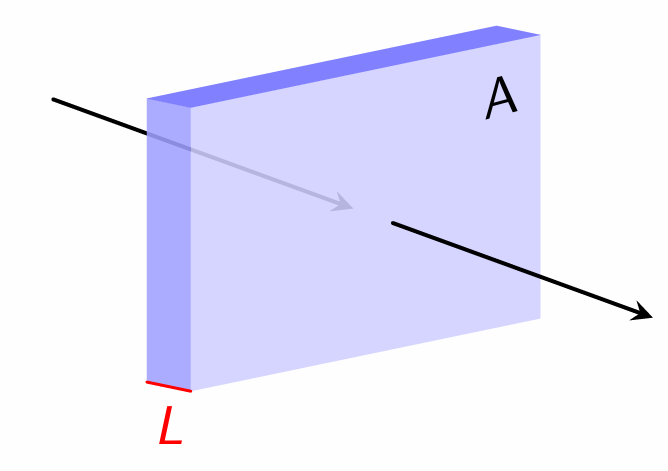
Consider the system shown above. The top, bottom, front and back of the cube are insulated, so that heat can be conducted through the cube only in the \(x\) direction. In this special case, heat flow is one dimensional. If sides were not insulated, heat flow could be two or three dimensional.

Boundary conditions: \[\begin{aligned} {2} T &= T_1 \qquad \text{at} \quad x&=0 \\ T &= T_2 \qquad \text{at} \quad x&=L \end{aligned}\]


\[\frac{d}{d x}\left(\frac{d T}{\partial x}\right) = 0\] Intergrating , we get \[\frac{dT}{dx} = C_1 \tag*{(1)}\] Intergrating further, we get \[T = C_1x + C_2 \tag*{(2)}\]

Using the boundary condition at \(x=0\) gives \[C_2=T_1\] And, from the boundary condition at \(x=L\) gives, \[T_2 = C_1 L + T_1 \qquad \Longrightarrow \quad C_1 = \frac{T_2-T_1}{L}\]

Substituting for \(C_1\) in Eqn.(1), we get \[\frac{dT}{dx} = \frac{T_2-T_1}{L} \] From the definition of heat flux (as given by Fourier's law) \[ q = -k\frac{dT}{dx} \] Therefore, \[ q = -k\frac{T_2-T_1}{L} = k\frac{T_1-T_2}{L} \] \[ Q = qA =kA\frac{T_1-T_2}{L} = \frac{T_1-T_2}{R} \] where \[ \boxed{R =\frac{L}{kA}} \] \(R\) is called the thermal resistance of the flat plate for heat flow through an area of \(A\) across a temperature difference of \(T_1-T_2\).