7. One Dimensional Steady State Heat Conduction through Cylindrical Surface




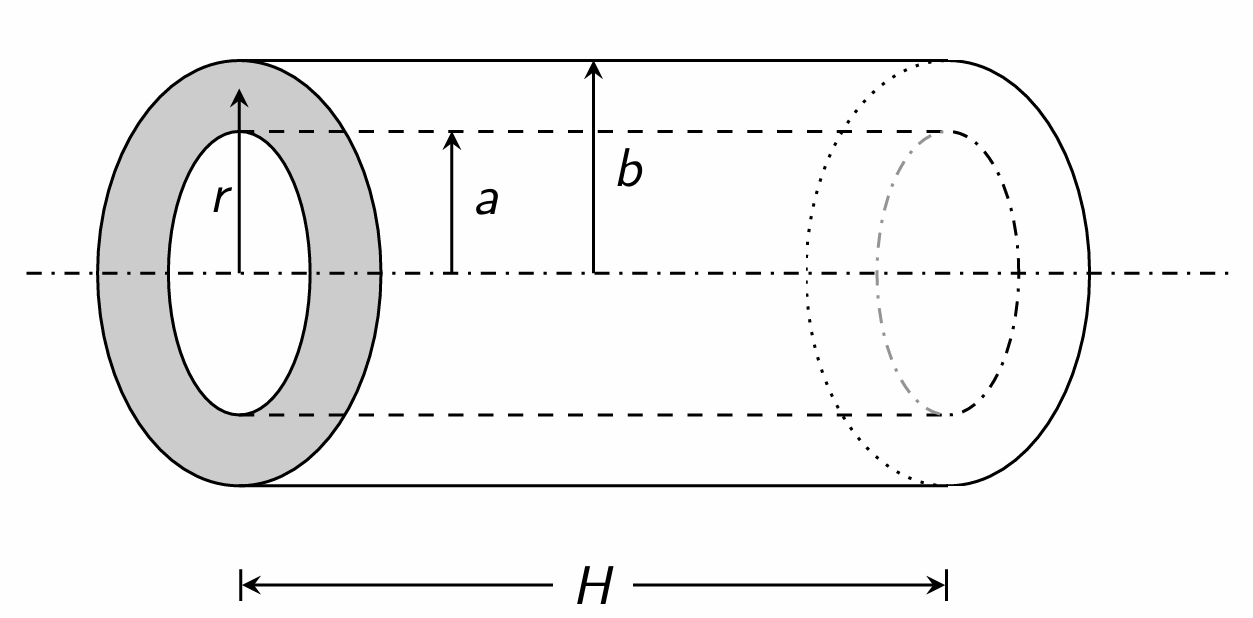
\[\begin{aligned} {2} T &= T_1 \qquad \text{at} \quad r&=a \\ T &= T_2 \qquad \text{at} \quad r&=b \end{aligned}\]

\[ \frac{d}{d r}\left(r \frac{d T}{\partial r}\right) = 0 \] Intergrating , we get \[ r\frac{dT}{dr} = C_1 \] i.e., \[ \frac{dT}{dr} = \frac{C_1}{r} \tag*{(1)} \] Intergrating further, we get \[ T = C_1\ln r + C_2 \tag*{(2)} \] Using the boundary condition at $r=a,b$ gives \begin{align*} T_1 &= C_1\ln a + C_2 \tag*{(3)}\\ T_2 &= C_1\ln b + C_2 \tag*{(4)} \end{align*}


*[-30pt] \[\text{Eqn.(4) $-$ Eqn.(3) $\Longrightarrow$} \qquad T_2-T_1 = C_1(\ln b - \ln a) \qquad \ \] i.e., \[C_1 = -\frac{T_1-T_2}{\ln(b/a)} \tag*{(5)}\] Using Eqn.(5) in Eqn.(1), we get \[\frac{dT}{dr} = \frac{C_1}{r} = -\frac{1}{r}\frac{T_1-T_2}{\ln(b/a)}\] From the definition of heat flux, \(q = -k\frac{dT}{dr}\) And, from \(Q=qA=q(2\pi r H)\), we get \[Q = 2\pi k H \frac{T_1-T_2}{\ln(b/a)} = \frac{T_1-T_2}{R}\] where \[\boxed{R = \frac{\ln(b/a)}{2\pi k H}}\]