13 - Conduction - Multiple Resistances
Completion requirements
5. Composite Hollow Cylinder
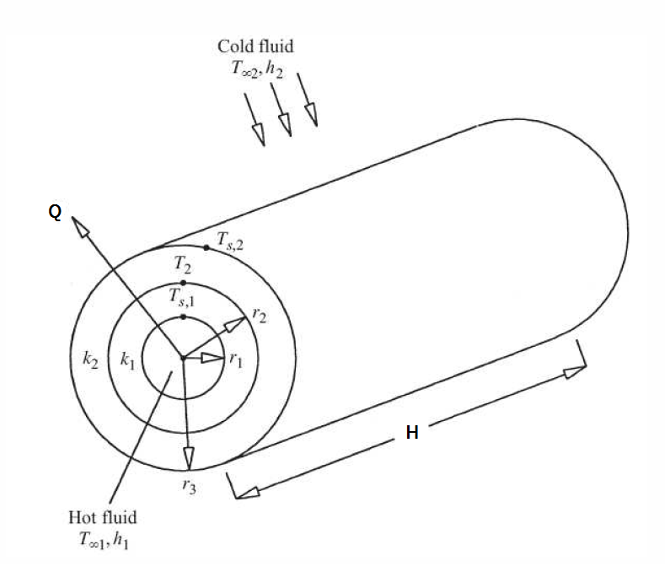
\[Q = \frac{T_{\infty_1}-T_{\infty,2}}{R_1+R_2+R_3+R_4}\] where \[R_1 = \frac{1}{h_12\pi r_1H} \quad \ R_2 = \frac{\ln(r_2/r_1)}{2\pi k_1H} \quad \ R_3=\frac{\ln(r_3/r_2)}{2\pi k_2H} \quad \ R_4 = \frac{1}{h_22\pi r_2H}\]
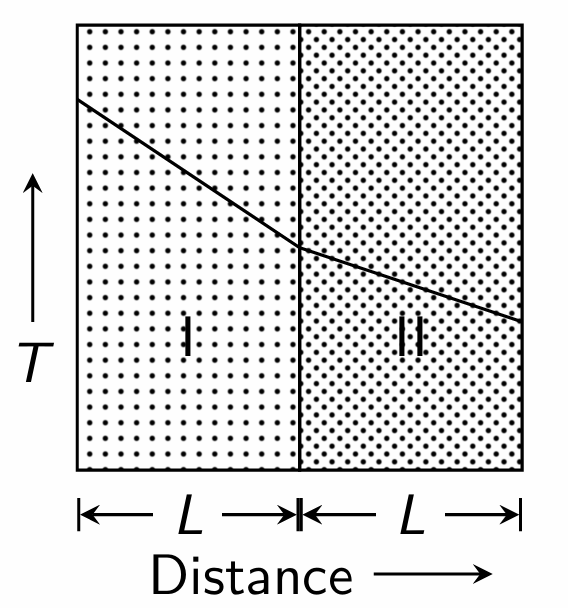
Then, the thermal conductivity of material I
1997-2.09
(a) is smaller than that of II
(b) is greater than that of II
(c) is equal to that of II
(d) can be greater than or smaller than that of II
(a) Explanation: \(q = k\, \dfrac{\Delta T}{\Delta x} = k\times \text{slope} = \text{const.}\) Here, \(\text{slope}_{\text{I}} > \text{slope}_{\text{II}}\). Therefore \(k_{\text{I}} < k_{\text{II}}\).
