13 - Conduction - Multiple Resistances
6. Solved Problems
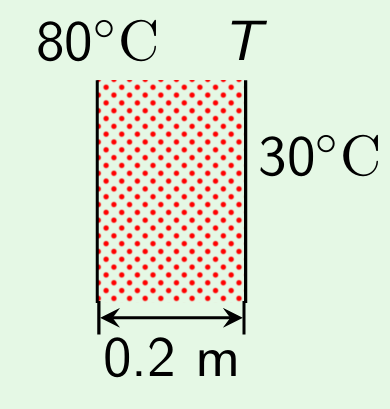
Example 1: Conduction followed by Convection The left face of a one dimensional slab of thickness 0.2 m is maintained at 80\( \circ \) C and the right face is exposed to air at 30\( \circ \) C. The thermal conductivity of the slab is 1.2 W/(m.K) and the heat transfer coefficient from the right face is 10 W/(m\(2\).K). At steady state. the temperature of the right face in \( \circ \)C is
2004-58
(a) 77.2 (b) 71.2 (c) 63.8 (d) 48.7
Example 2: Composite Wall The inner wall of a furnace is at a temperature of 700\( \circ \) C.The composite wall is made of two substances, 10 and 20 cm thick with thermal conductivities of 0.05 and 0.1\( \circ \) C W/m. respectively. The ambient air is at 30\( \circ \) C and the heat transfer coefficient between the outer surface of wall and air is 20 W/m2.\( \circ \) C. The rate of heat loss from the outer surface in W/m2 is
2003-57
(a) 165.4 (b) 167.5 (c) 172.8 (d) 175
\(q = \dfrac{\Delta T}{R}\), where \[R = \frac{x_1}{k_1} + \frac{x_2}{k_2} + \frac{1}{h} = \frac{0.1}{0.05} + \frac{0.2}{0.1} + \frac{1}{20} = 4.05 \text{\deg C.m$^2$/W}\] Therefore, \( q=\frac{\Delta T}{R} = \frac{(700-30)}{4.05} = {165.4 \text{ W/m$^2$}}\)
