7. Solved Problems

Example 3: Heat Loss Reduction by Thermopane A thermopane window consists of two sheets of glass each 6 mm thick, separated by a layer of stagnant air also 6 mm thick. Find the percentage reduction in heat loss from this pane as compared to that of a single sheet of glass 6 mm thickness. The temperature drop between inside and outside remains same at 15\( \circ \) C Thermal conductivity of glass is 30 times that of air.

(G-1988-14.iii)


Solution:






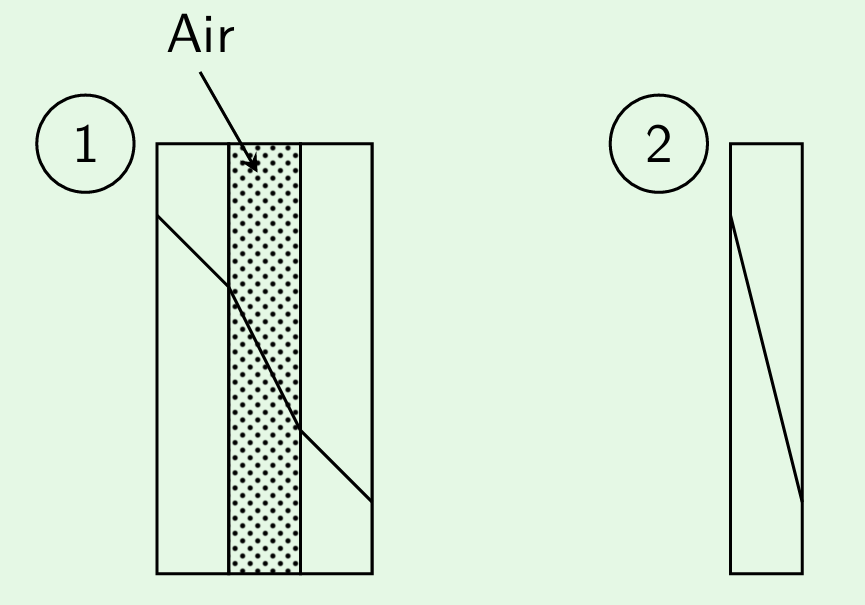
\[q = \frac{\Delta T}{L/k}\] Let \(k\) be the thermal conductivity of glass. Then, thermal conductivity of air = \(k/30\). \[\begin{aligned} q_1 &=& \frac{15}{\dfrac{6}{k} + \dfrac{6\times30}{k} + \dfrac{6}{k}} = \frac{15}{192}k \\ q_2 &=& \frac{15}{6/k} = \frac{15}{6}k \end{aligned}\] \[\begin{aligned} \text{Reduction in heat loss} &= \frac{q_2-q_1}{q_2} \times 100 \\ &= \frac{(15/6) - (15/192)}{(15/6)} \times 100 = {96.9\%} \end{aligned}\]

Example 4: Heat Transfer Through Cylindrical Surface Heat is generated at a steady rate of 100 W due to resistance heating in a long wire (length = 5 m, diameter = 2 mm). This wire is wrapped with an insulation of thickness 1 mm that has a thermal conductivity of 0.1 W/m.K. The insulated wire is exposed to air at 30\( \circ \) C. The convective heat transfer between the wire and surrounding air is characterized by a heat transfer coefficient of 10 W/m\(^2\).K. The temperature (in \( \circ \) C ) at the interface between the wire and the insulation is

(G-2012-34)

(a) 211.2 (b) 242.1 (c) 311.2 (d) 484.2

Solution:

Rate of heat transfer from a cylindrical surface is given by \[Q = \frac{\Delta T}{R} = \frac{T_1-T_2}{\left(\dfrac{t}{kA_m} \right)_{\text{ins}} + \left(\dfrac{1}{h_2A_2} \right)}\] where
\(t\) = \((r_2-r_1)\), thickness of insulation, and
\(A_m\) =  \(A_{lm}=\dfrac{A_2-A_1}{\ln(A_2/A_1)} = \dfrac{2\pi(r_2-r_1)L}{\ln(r_2/r_1)}\)

Therefore, \[A_m = \frac{2\pi(r_2-r_1)L}{\ln(r_2/r_1)} = \frac{2\times\pi\times(0.002-0.001)\times5}{\ln(0.002/0.001)} = 0.0453 \text{ m$^2$}\] Using this and subsituting the known values in the equation for \(Q\), we get \[100 = \frac{T_1-30}{\left(\dfrac{0.001}{0.1\times0.0453} \right) + \left(\dfrac{1}{10\times(2\pi\times0.002\times5)} \right)}\] Solving the above, we get T1= 211.2 \( \circ \) C. (a).