14 - Conduction - Critical Radius of Insulation

Cylindrical surface:

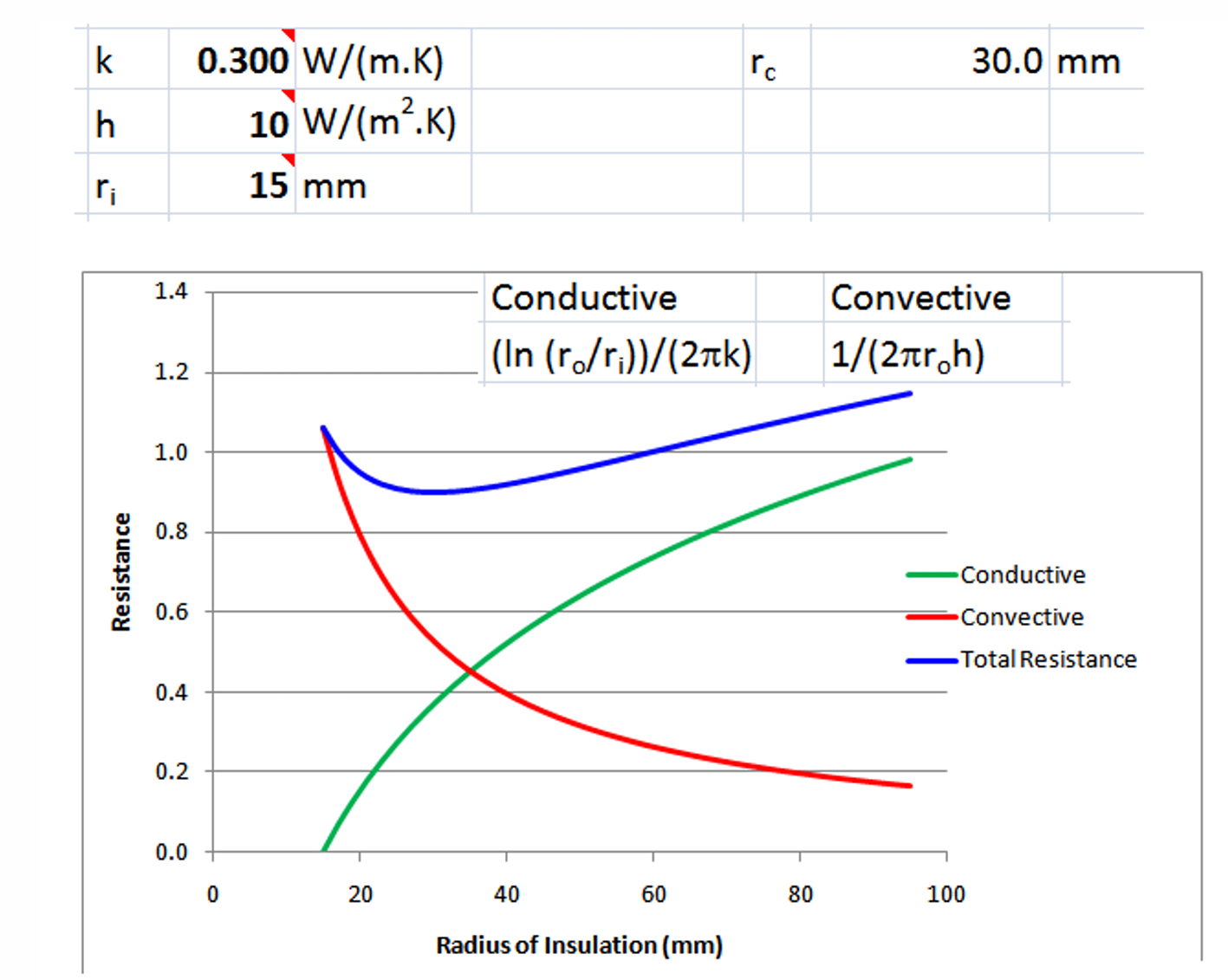
\[Q = \frac{T_i-T_{\infty}}{R} = \frac{T_i-T_{\infty}}{R_{\text{ins}}+R_o}\] where \[R_{\text{ins}} = \frac{\ln(r_o/r_i)}{2\pi k H} \qquad \text{ and } \qquad R_o = \frac{1}{2\pi r_o H h}\] \(Q\) may have a maximum for a certain value of \(r_o=r_{oc}\). This critical value is obtained by differentiating \(Q\) with respect to \(r_o\), and setting the resulting expression to zero. \[Q = \frac{(T_i-T_{\infty})2\pi kH}{\ln\left(\dfrac{r_o}{r_i}\right) + \dfrac{k}{hr_o}}\] \[\frac{dQ}{dr_o} = 0 \qquad \Longrightarrow \quad \frac{d}{d r_o}\left[{\ln\left(\dfrac{r_o}{r_i}\right) + \dfrac{k}{hr_o}} \right] = 0\]

\[\frac{d}{d r_o}\left[\ln\left(\dfrac{r_o}{r_i}\right) + \dfrac{k}{hr_o} \right] =\frac{d}{d r_o}\left[{\ln r_o - \ln r_i + \dfrac{k}{hr_o}} \right] = \frac{1}{r_o} - \frac{k}{hr_o^2}\] Equating the above to zero (at \(r_o=r_{oc}\)), gives \[\frac{1}{r_{oc}} - \frac{k}{hr_{oc}^2} = 0 \qquad \Longrightarrow \quad \boxed{r_{oc} = \frac{k}{h}}\]