15 - Conduction - Fins
3. Overall Heat Transfer Coefficient (U)
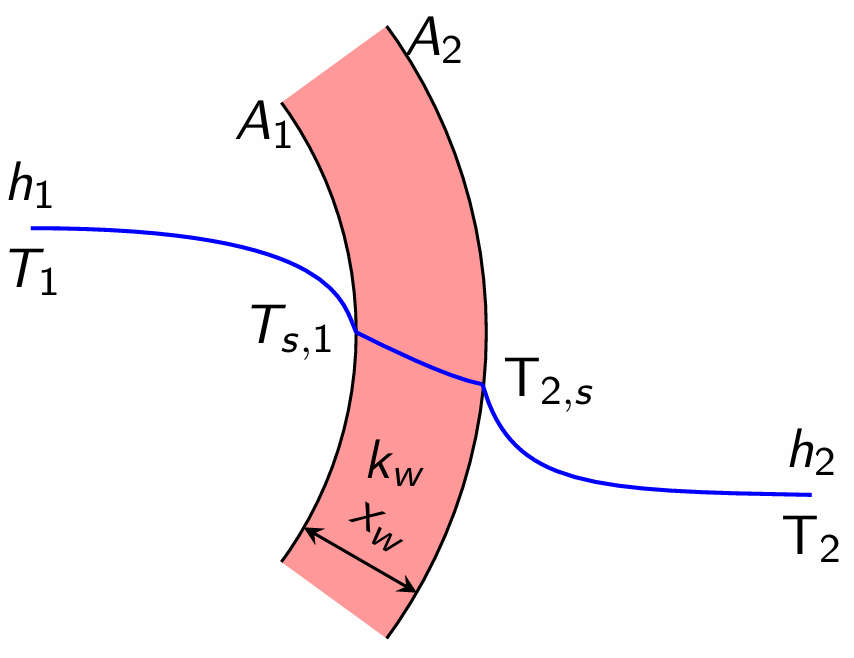
\[T_1 - T_{1,s} = \frac{Q}{h_1A_1} \qquad T_{1,s}-T_{2,s} = \frac{x_wQ}{k_wA_m} \qquad T_{2,s}-T_2= \frac{Q}{h_2A_2}\] Adding the numerator and denominator separately, we get \[T_1-T_2= \Delta T = Q\left[\frac{1}{h_1A_1} + \frac{x_w}{k_wA_m} + \frac{1}{h_2A_2} \right]\] From the relation \(Q=U_1A_1\Delta T\), we get \[\frac{Q}{U_1A_1} = Q\left[\frac{1}{h_1A_1} + \frac{x_w}{k_wA_m} + \frac{1}{h_2A_2} \right]\] i.e., \[\frac{1}{U_1A_1} = \frac{1}{h_1A_1} + \frac{x_w}{k_w}\frac{A_1}{A_m} + \frac{1}{h_2A_2} = \frac{1}{U_2A_2}\]
For highly conducting and / or thin-walled tubes, we can neglect the conductive resistance part, and hence: \[\frac{1}{U_1A_1} = \frac{1}{h_1A_1} + \frac{1}{h_2A_2}\]

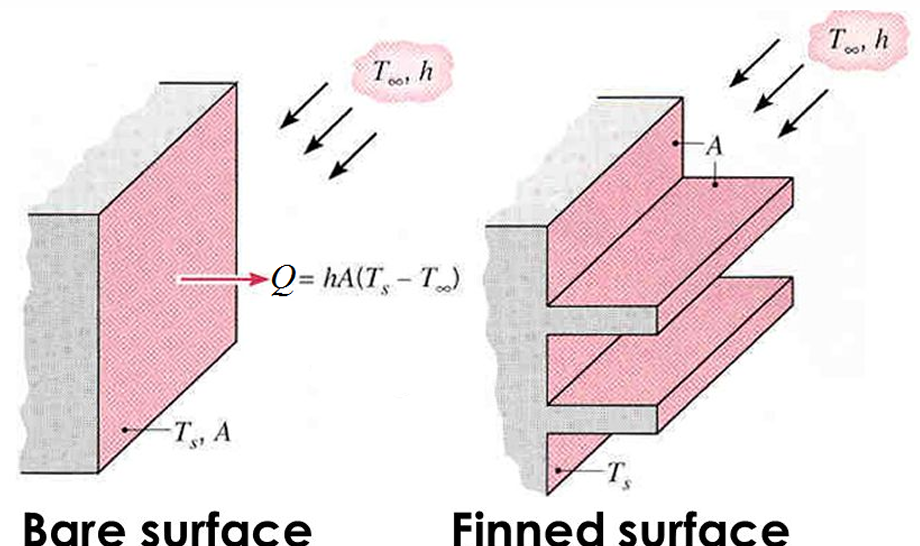
\[Q = hA(T_s - T_\infty)\] The rate of convective heat transfer from a surface at \(T_s\) can be increased by two methods:
-
increasing the convective heat transfer coefficient, \(h\)
-
increasing the surface area, \(A\)
Increasing the convective heat transfer coefficient may not be practical and/or adequate. An increase in surface area by attaching extended surfaces called fins to the surface is more convenient.


Examples of Extended Surfaces (Fins):
Thin rods on condenser in back of refrigerator
Honeycomb surface of a car radiator
Corrugated surface of a motorcycle engine
