15 - Conduction - Fins

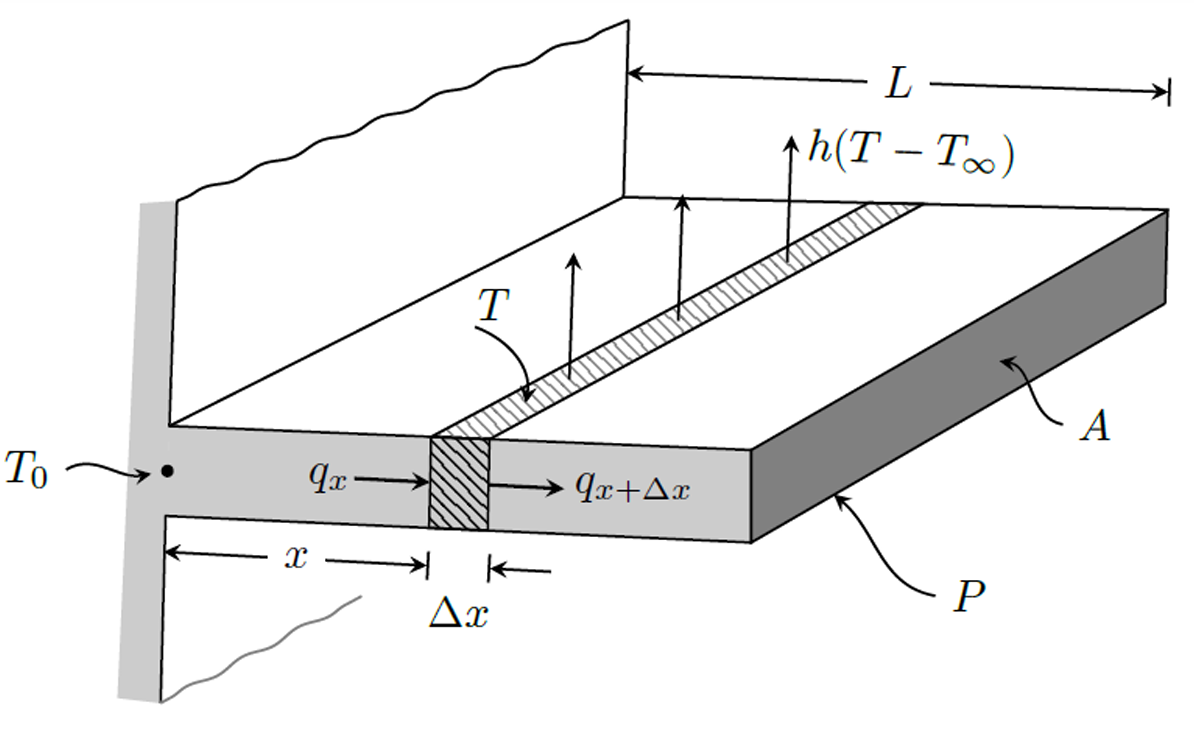
\[\begin{gathered} \text{Heat in at $x$ by conduction}= \text{Heat out by conduction at ($x+\Delta x$)} \\ + \text{Heat out by convection} \end{gathered}\]

i.e., \[\text{Net heat in by conduction} = \text{Heat out by convection}\] i.e., \[(Aq)|_x - (Aq)|_{x+\Delta x} = hP\Delta x (T-T_{\infty}) \tag*{(1)}\] Dividing throughout by \(\Delta x\), and, from the definition of derivative, (for \(\Delta x \rightarrow 0\)) \[-\frac{\left((Aq)|_{x+\Delta x} - (Aq)|_x \right)}{\Delta x} = -\frac{d(Aq)}{dx}\]

From Fourier’s law of conduction, \(q=-k\dfrac{dT}{dx}\). Therefore, \[-\frac{d(Aq)}{dx} = Ak\frac{d^2T}{dx^2}\] Using this in Eqn.(1), we get \[Ak\frac{d^2T}{dx^2} = hP(T-T_{\infty})\] i.e., \[\frac{d^2T}{dx^2} -\frac{hP}{Ak}(T-T_{\infty}) = 0\] or, \[\boxed{\frac{d^2\theta}{dx^2} -m^2\theta = 0}\] where \[m^2 = \frac{hP}{Ak} \qquad \text{ and } \qquad \theta = (T-T_\infty)\]

\[\frac{d^2\theta}{dx^2} -m^2\theta = 0\] The above equation is a linear homogeneous, second-order ordinary differential equation. The solution of which is given by \[\begin{aligned} \theta &= C_1e^{-mx} + C_2e^{mx} {Or,} \theta&= C_1' \cosh mx + C_2' \sinh mx {Or,} \theta&= C_1'' \cosh m(L-x) + C_2'' \sinh m(L-x) \end{aligned}\]