9. Fin Efficiency


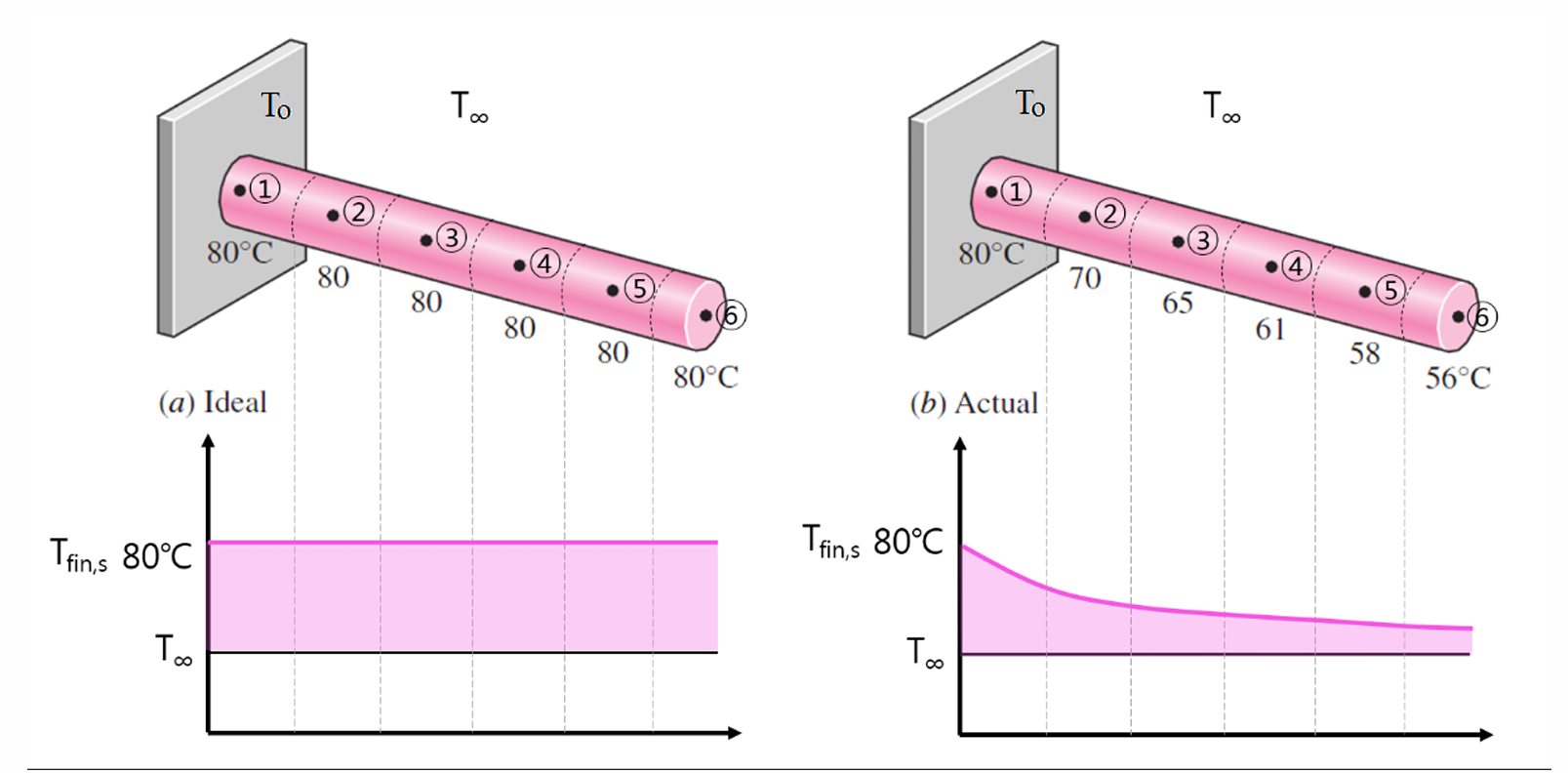
Temperature of a fin gradually drops along the length. In the limiting case of zero thermal resistance (\(k\rightarrow \infty\)), the temperature of the fin will be uniform at the base value of \(T_o\). The heat transfer from the fin will be maximized in this case: \[Q_{\text{fin,max}} = hA_{\text{fin}}(T_o-T_\infty)\] Fin efficiency (\(\eta_{\text{fin}}\)) can be defined as: \[\eta_{\text{fin}} = \frac{Q_{\text{fin}}}{Q_{\text{fin,max}}} = \frac{\text{actual heat transfer rate from the fin}}{\begin{array}{c}\text{ideal heat transfer rate from the fin}\\ \text{(if the entire fin were at base temperature)}\end{array}}\] Fin efficiency decreases with increasing fin length because of decrease in fin temperature with length.

For the long-fin \[\eta_{\text{fin}} = \frac{Q_{\text{fin}}}{Q_{\text{fin,max}}} = \frac{\sqrt{PhkA}(T_o-T_\infty)}{hA_f(T_o-T_\infty)} = \frac{\sqrt{PhkA}}{hPL} = \frac{1}{L}\sqrt{\frac{kA}{hP}} = \frac{1}{mL}\]