15 - Conduction - Fins

\[\theta = C_1e^{-mx} + C_2e^{mx} \tag*{(1)}\] i.e., at \(x=0\), \(T=T_o\); and, at \(x=L\), \(T=T_L\).

B.C.: \[\begin{aligned} {3} \theta &=\theta_o \qquad & \text{ at } x&=0 \\ \theta &=\theta_L \qquad & \text{ at } x&=L \end{aligned}\] Using B.C 1 in Eqn.(1), we get \[\theta_o = C_1 + C_2 \qquad \Longrightarrow \quad C_1 = \theta_o - C_2 \tag*{(2)}\] And, using B.C 2 in Eqn.(1), we get \[\theta_L = C_1e^{-mL} + C_2e^{mL} \tag*{(3)}\]

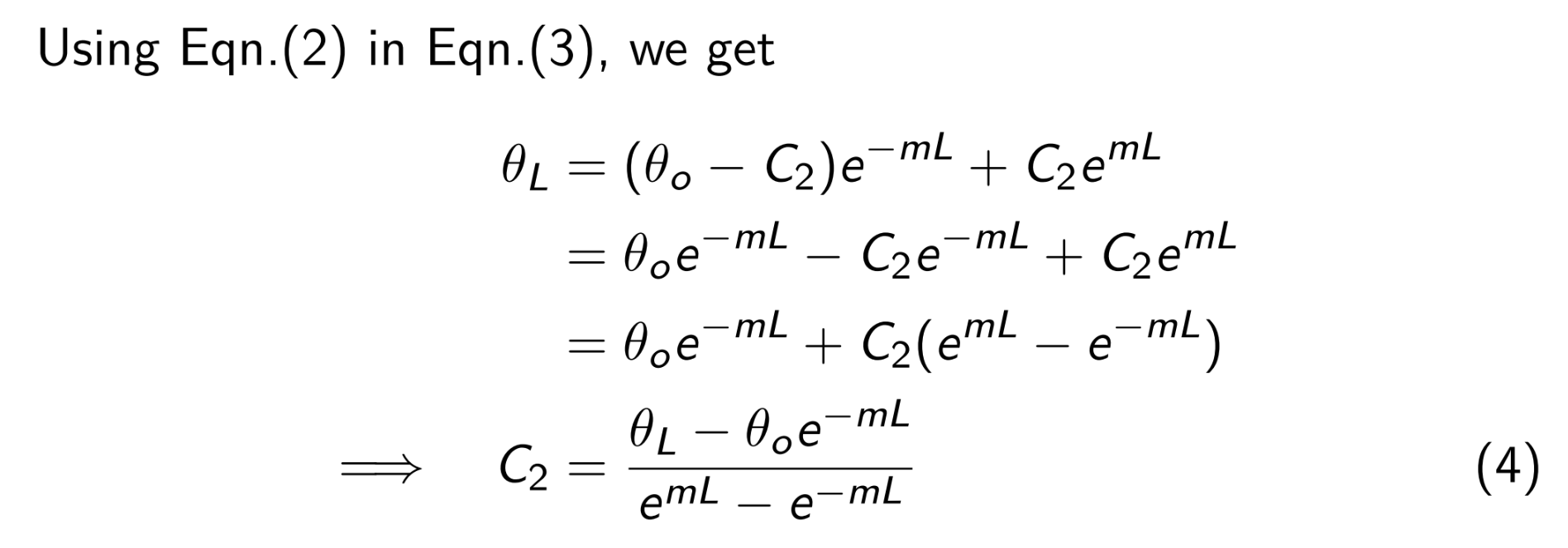
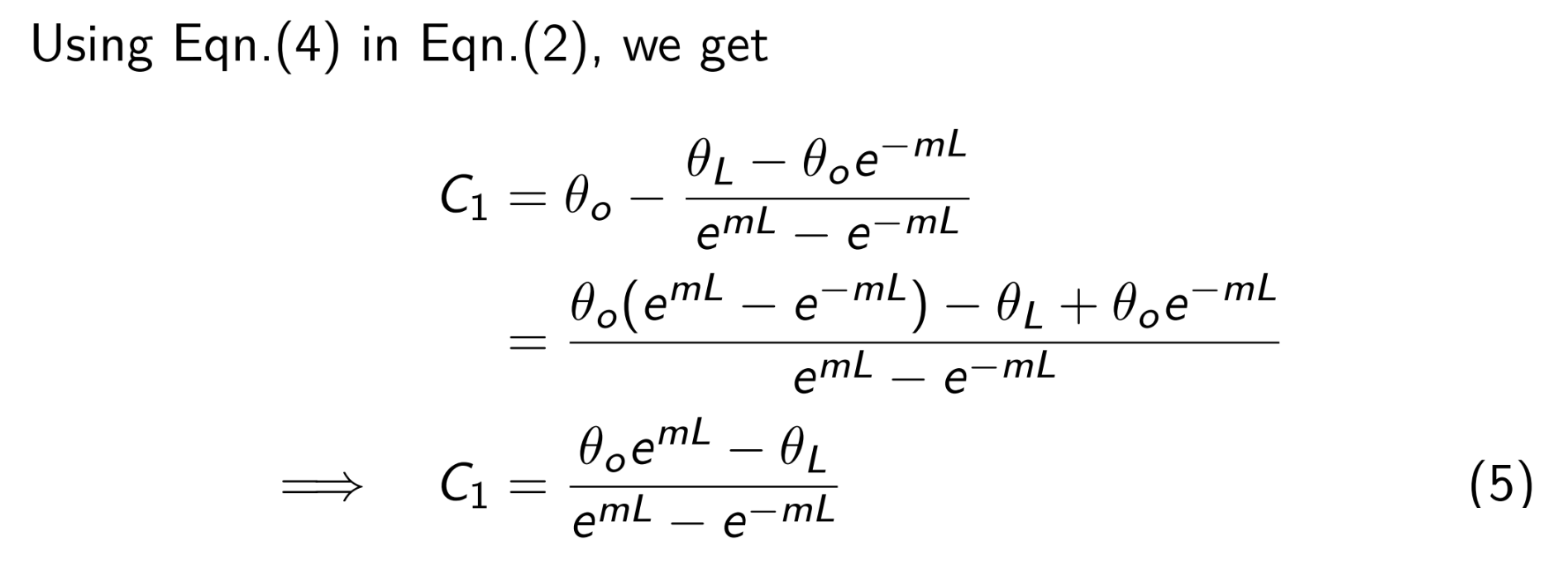
Substituting for \(C_1\) and \(C_2\) in Eqn.(1), we get \[\begin{aligned} \theta &= \frac{\theta_oe^{mL}-\theta_L}{e^{mL}-e^{-mL}} e^{-mx} + \frac{\theta_L-\theta_oe^{-mL}}{e^{mL}-e^{-mL}}e^{mx} \\ &=\frac{\theta_oe^{mL}e^{-mx} - \theta_oe^{-mL}e^{mx} + \theta_Le^{mx} - \theta_Le^{-mx}}{e^{mL}-e^{-mL}} \\ &= \frac{\theta_o\left(e^{m(L-x)} - e^{-m(L-x)}\right)+\theta_L(e^{mx}-e^{-mx})}{e^{mL}-e^{-mL}} \end{aligned}\] We know, \[\frac{e^{mx}-e^{-mx}}{2} = \sinh mx\] Using this in above, we get \[\boxed{\theta = \frac{\theta_o\sinh m(L-x)+\theta_L\sinh mx}{\sinh mL}}\]