15 - Conduction - Fins
15. Solved Problem
Fin with Adiabatic Tip An aluminum pot is used to boil water as shown below. The handle of the pot is 20 cm long, 3 cm wide, and 0.5 cm thick. The pot is exposed to room air at 25oC, and the convection coefficient is 5 W/m2.oC.. Can you touch the handle when the water is boiling? What would be the temperature near the end of the handle? (\(k\) for aluminum is 237 W/(m.oC)
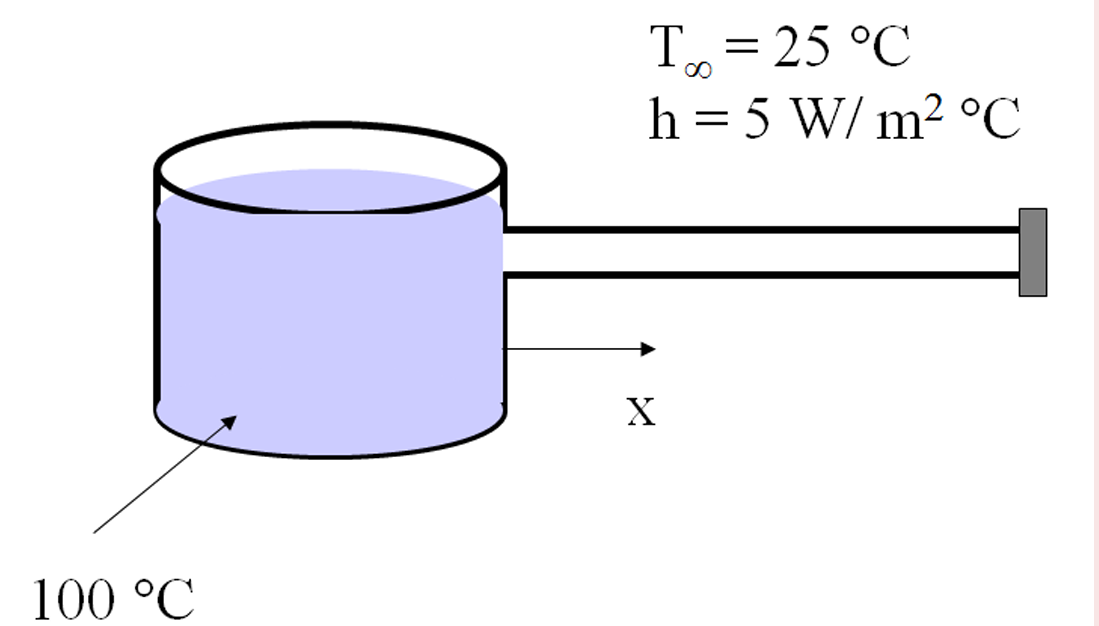
Solution: We can model the pot handle as an extended surface. Assume that there is no heat transfer at the free end of the handle. For this case, \[\frac{T-T_\infty}{T_o-T_\infty} = \frac{\cosh m(L-x)}{\cosh mL}\] where \[m = \sqrt{\frac{Ph}{kA}}\] Here, \(h=5\) W/m\(^2\)., \(P=2(W+B)=2(0.03+0.005)=0.07\) m, \(k=237\) W/m., \(A=WB=0.03\times0.005=0.00015\) m\(^2\), and \(L=0.2\) m.
Therefore, \[m=\sqrt{\frac{Ph}{kA}}= \sqrt{\frac{0.07\times5}{237\times0.00015}} = 3.138\]
Hence, \[\begin{aligned} \frac{T-T_\infty}{T_o-T_\infty} &= \frac{\cosh m(L-x)}{\cosh mL} \\ \frac{T-25}{100-25} &= \frac{\cosh \bigl(3.138\times(0.2-0.2)\bigr)}{\cosh(3.138\times0.2)} \\ \Longrightarrow \quad T(x=0.2) &= 87.3^\circ\text{C} \end{aligned}\] Since \(T\) near the end is \(87.3^\circ\)C, it is not safe to touch the end.
If a stainless steel handle is used instead, what will happen? For stainless steel, the thermal conductivity \(k=15\) W/m. (Ans: 37.3; safer than the previous case)
