16 - Conduction - Heat Generation

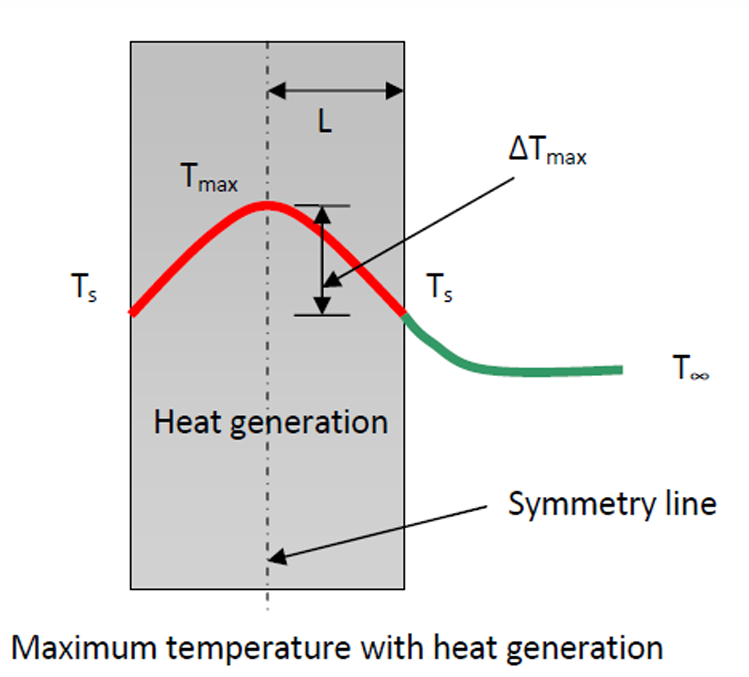
The maximum temperature \(T_{\text{max}}\) in a solid with uniform heat generation will occur at a location furthest away from the outer surfaces when the outer surface is maintained at a constant temperature of \(T_s\).

Consider a solid medium of surface area \(A\), volume \(V\), and constant thermal conductivity \(k\), where heat is generated at a constant rate of \(\dot{g}\) per unit volume. Heat is transferred from the solid to the surrounding medium at \(T_\infty\). Under steady conditions, the energy balance for the solid can be expressed as: \[\begin{aligned} \begin{array}{c}\text{rate of heat transfer} \\ \text{from the solid} \end{array} &= \begin{array}{c}\text{rate of heat generation} \\ \text{within the solid} \end{array}\\ Q &= \dot{g}V {For the heat transfer at the surface,} hA(T_s-T_\infty) &= \dot{g}V \\ \Longrightarrow \quad T_s &= \frac{\dot{g}V}{hA} + T_\infty \end{aligned}\]

Using the above relationship, the surface temperature can be calculated for a plane wall of thickness \(2L\), a long cylinder of radius \(r_o\) and a sphere of radius \(r_o\), as follows: \[\begin{aligned} T_{\text{s, plane wall}} &= \frac{\dot{g}L}{h} + T_\infty \\ T_{\text{s, cylinder}} &= \frac{\dot{g}r_o}{2h} + T_\infty \\ T_{\text{s, sphere}} &= \frac{\dot{g}r_o}{3h} + T_\infty \end{aligned}\]