8-Conduction - Unsteady Heat Conduction
3. Lumped Parameter Formulation
A lumped parameter formulation is an approximation which facilitates the solution of heat transfer problems. The key assumption is the neglect of temperature gradients (\(dT/dx\)) inside the body of volume \(V\) and surface area \(A\), so that its temperature is only a function of time. However, this assumption clearly amounts to the neglect of the heat conduction processes inside the material and should be used with caution.
This approximation is valid if \[\text{Bi} = \frac{hL}{k} < 0.1\] where \(L=V/A\)
If the only mechanism for energy exchange with the surroundings is convection through the bounding surface, the differential thermal energy balance equation (in W) becomes \[-hA(T-T_{\infty}) = \rho C_P V\frac{dT}{dt}\] This is a first order ordinary differential equation which can be solved easily. Rearranging the above, \[\begin{aligned} \frac{dT}{dt}+\frac{hA}{\rho C_P V}(T-T_{\infty}) &= 0 \\ \frac{dT}{dt}+m(T-T_{\infty}) &= 0 \end{aligned}\] where \[m = \frac{hA}{\rho C_P V}\]
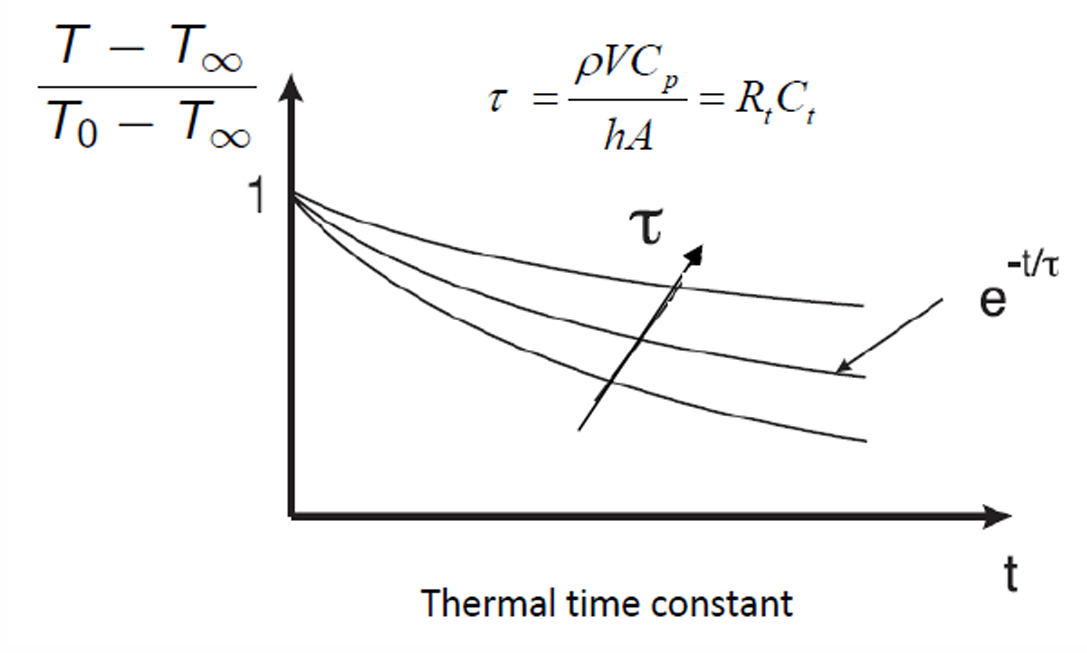
Let \(\theta=T-T_\infty\). Then, \(\dfrac{d\theta}{dt}=\dfrac{dT}{dt}\). Therefore, \[\frac{d\theta}{dt} + m\theta=0\] Solution of the above ODE is given by \[\frac{d\theta}{\theta} = -mdt\] Integrating, \[\ln\theta = -mt + C_1\] Initial condition: At \(t=0\), \(\theta=\theta_0 = T_0-T_\infty\). Substituting this in the above, we get \[\ln\theta_0 = C_1\] Hence, \[\ln\theta = -mt + \ln\theta_0 \qquad \Longrightarrow \quad {\frac{\theta}{\theta_0} = e^{-mt}}\]
\[\frac{T-T_{\infty}}{T_0-T_\infty} = e^{-mt}\] \[m = \frac{hA}{\rho C_P V}= \frac{1}{\tau}\]