8-Conduction - Unsteady Heat Conduction
4. Biot Number
\[\text{Bi} = \frac{hL}{k} = \frac{\text{resistance to internal heat flow}}{\text{resistance to external heat flow}}\] Whenever the Biot number is small, the internal temperature gradients are also small and a transient problem can be treated by the“lumped thermal capacity” approach. The lumped capacity assumption implies that the object for analysis is considered to have a single temperature.
\[\frac{T_H-T_S}{T_S-T_\infty} = \frac{L/(kA)}{1/(hA)} = \frac{\text{internal resistance to H.T}}{\text{external resistance to H.T}} = \frac{hL}{k} = \text{Bi}\]
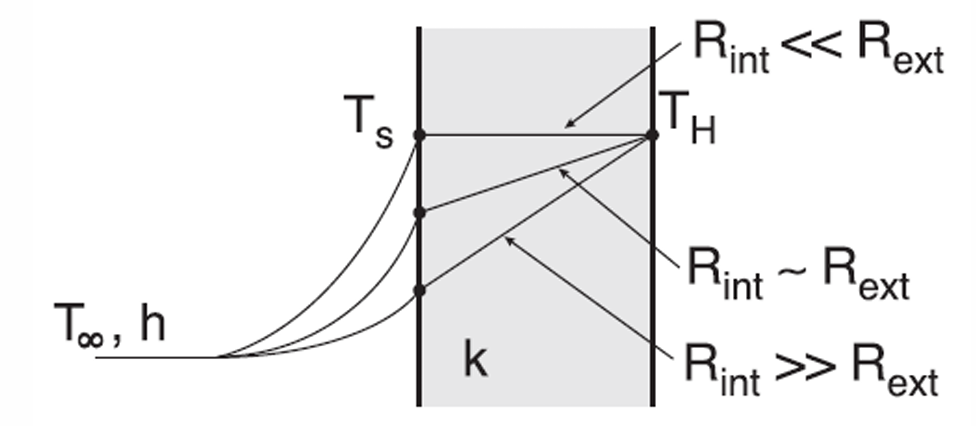
\(R_{\text{int}}\ll R_{\text{ext}}\): the Biot number is small and we can conclude \[T_H-T_S \ll T_S-T_\infty \qquad \text{ and in the limit } T_H \approx T_S\] \(R_{\text{ext}}\ll R_{\text{int}}\): the Biot number is large and we can conclude \[T_S-T_\infty \ll T_H-T_S \qquad \text{ and in the limit } T_S \approx T_\infty\]
A 150 micrometer diameter steel sphere of \(\rho = 7,700\) kg/m\(^3\), \(C_P = 460\) J/(kg.K), \(k = 25\) W/(m.K) is quenched from a temperature of 1200 K using an air jet with \(h = 100\) W/(m\(^2\).K), at room temperature (\(T_{\infty} = 300\) K). Calculate the value of Bi for this system and, if possible, use the lumped parameter model to estimate the time it takes for the temperature of the sphere to reach 325 K.
