9. Heisler Chart Usage - Solved Problem

Example 1: Transient Heat Transfer in Cylinder A 2 m long 0.2 m diameter steel cylinder (\(k=40\) W/m.K, \(\alpha=1\times10^{-5}\) m\(^2\)/s, \(\rho=7854\) kg/m\(^3\), \(C_P=434\) J/kg.K), initially at 400oC, is suddenly immersed in water at 50oC for quenching process. If the convection coefficient is 200 W/m\(^2\).K, calculate after 20 minutes:

  • the center temperature

  • the surface temperature

  • the heat transfer to the water

Solution: \(L/D=2/0.2=10\); we assume infinitely long cylinder.

Check Lumped Capacitance Method (LCM): \[\text{Bi}=\frac{hL}{k} = \frac{h(V/A)}{k} = \frac{h(r_o/2)}{k} = \frac{200 \times (0.1/2)}{40}=0.25\] Since \(\text{Bi}>0.25\), we can not use LCM, instead we can use Heisler charts.

From the definition of Bi as given in Heisler chart, \[Bi = \frac{hr_o}{k} = \frac{200\times0.1}{40} = 0.5 \qquad \Longrightarrow \quad \frac{1}{\text{Bi}}=\frac{1}{0.5}=2\] and, \[\text{Fo} = \tau = \frac{\alpha t}{r_o^2} = \frac{1\times10^{-5}\times(20\times60)}{0.1^2}=1.2\] \[\text{Bi}^2\tau = 0.5^2\times1.2 = 0.3\]

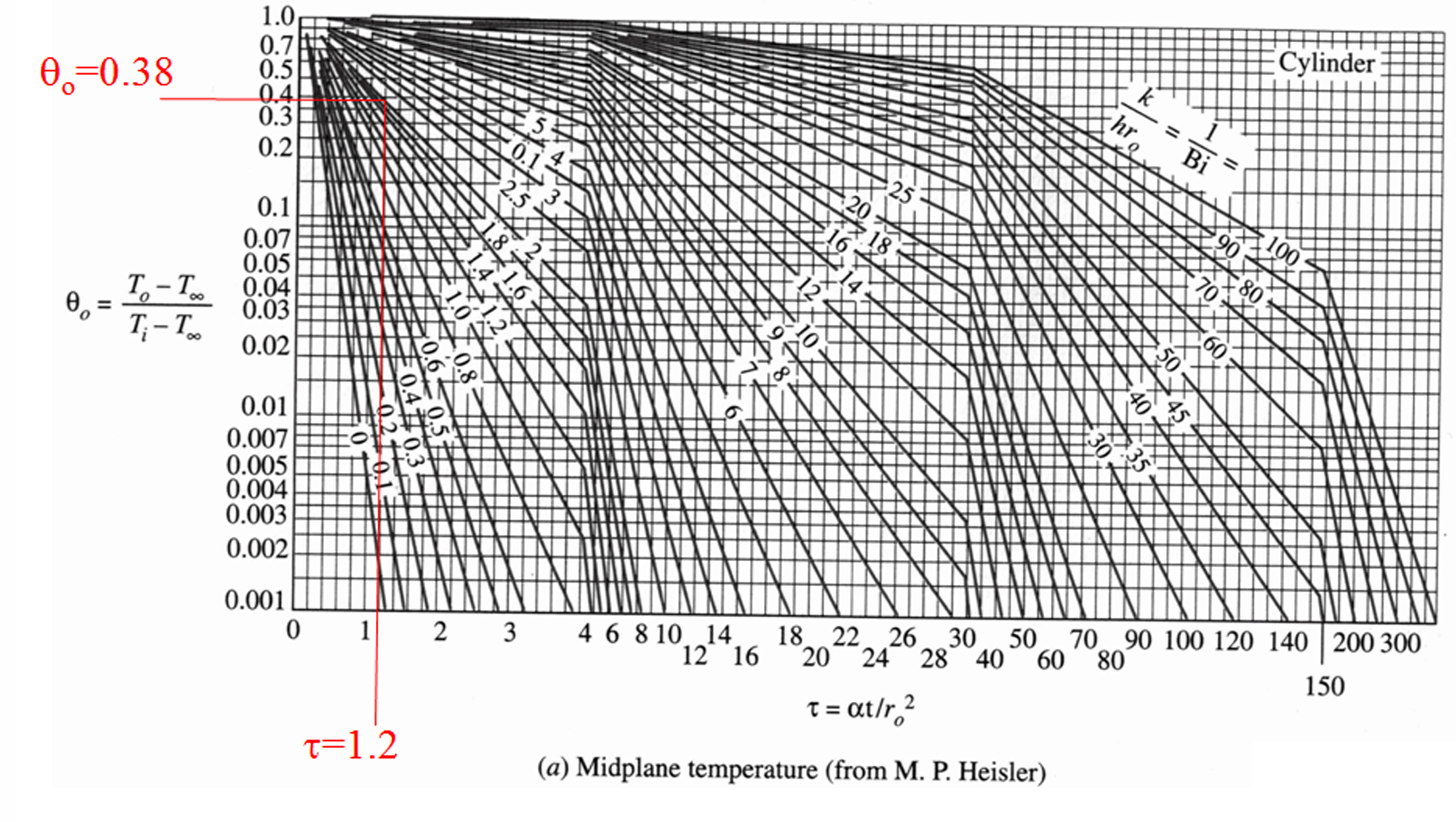
Centreline Temperature (\(T_0\)):

For \(1/\text{Bi}=2\), and \(\tau=1.2\), from figure (a), we get \(\theta_0=0.38\). \[\begin{aligned} \theta_0&=\frac{T_0-T_\infty}{T_i-T_\infty}=0.38 \\ \Longrightarrow \quad T_0&=(400-50)\times0.38+50=183^{\circ} C \end{aligned}\]


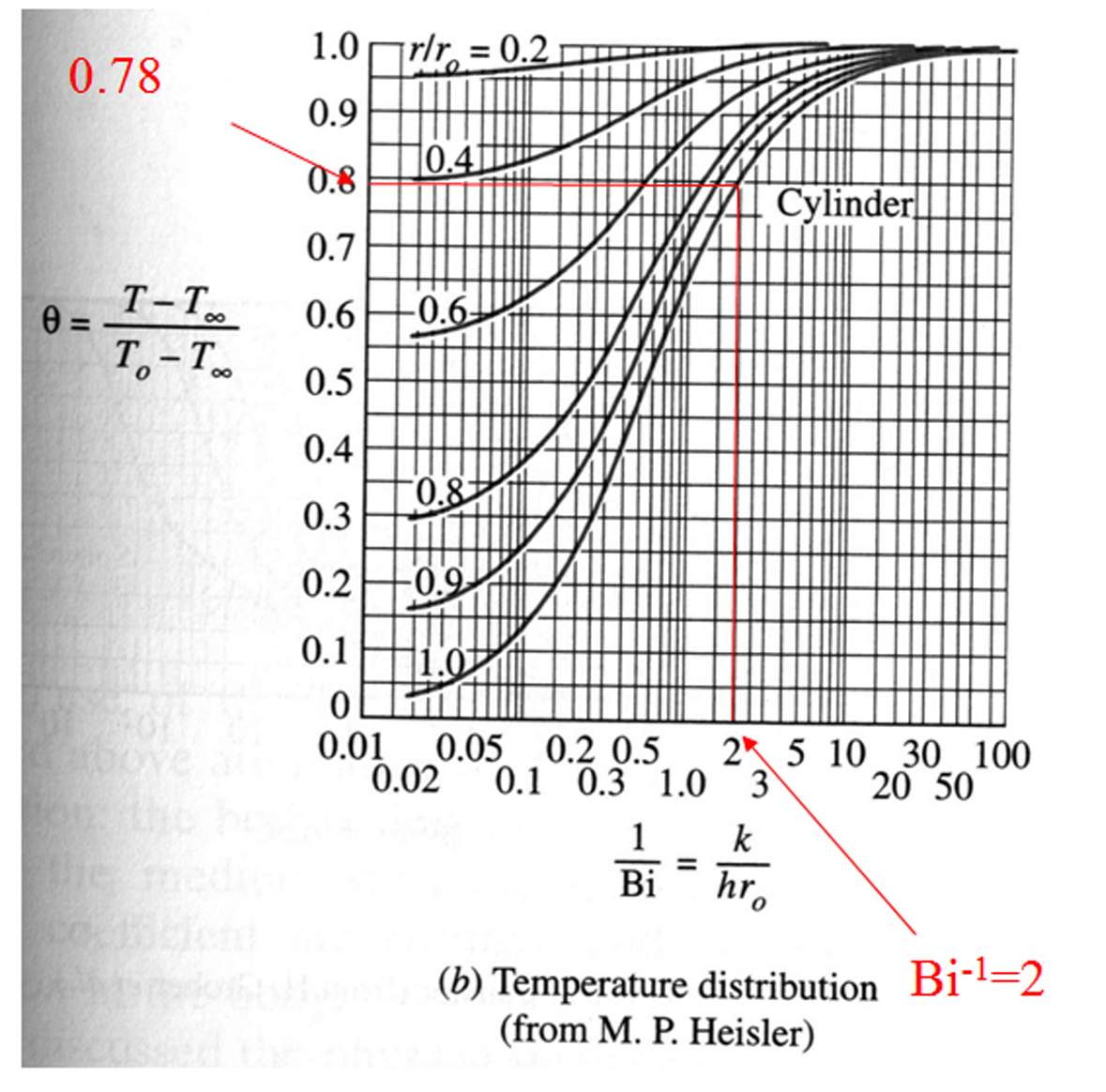
Surface Temperature (\(T\)):

For \(r/r_o=1\), and \(1/\text{Bi}=2\), from figure (b), we get \(\theta=0.78\). \[\begin{aligned} \theta &=\frac{T-T_\infty}{T_0-T_\infty}=0.78 \\ \Longrightarrow \quad T&=(183-50)\times0.78+50=153.74^{\circ}C \end{aligned}\]



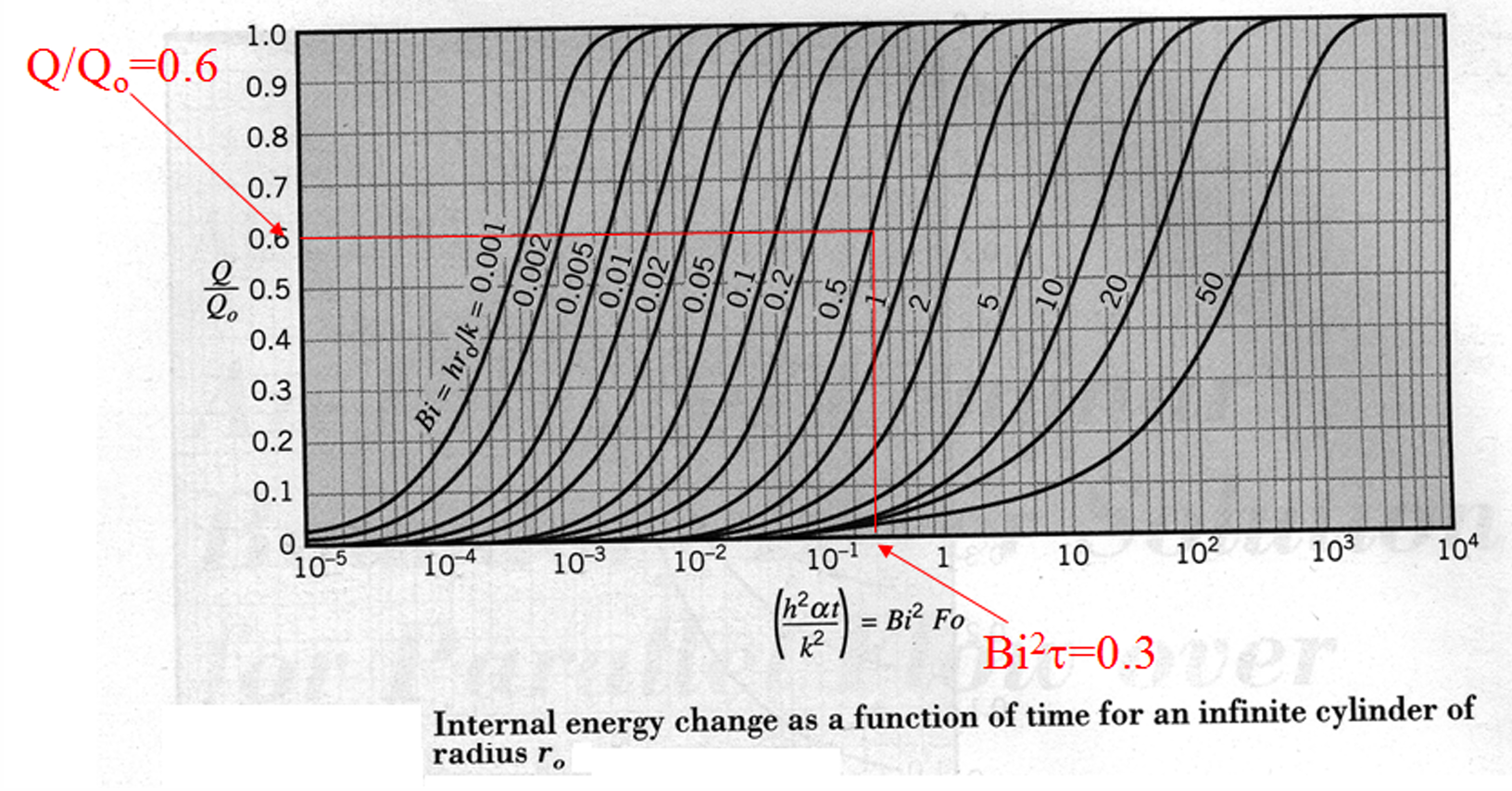
Heat Transfer (\(Q\)):

For \(\text{Bi}^2\tau=0.3\), and \(\text{Bi}=0.5\), from figure (c), we get \(Q/Q_0=0.6\). \[\begin{aligned} Q_0 &=\rho V C_P(T_i-T_\infty)\\ &=7854\times\bigl(\pi \times0.1^2\times2\bigr)\times434\times(400-50) \\ &= 7.5\times10^7 \text{ J} \\ Q&=Q_0\times0.6=4.5\times10^7 \text{ J} \end{aligned}\]