24 - Convection - Solved Problems
3. 3. Solved Problems
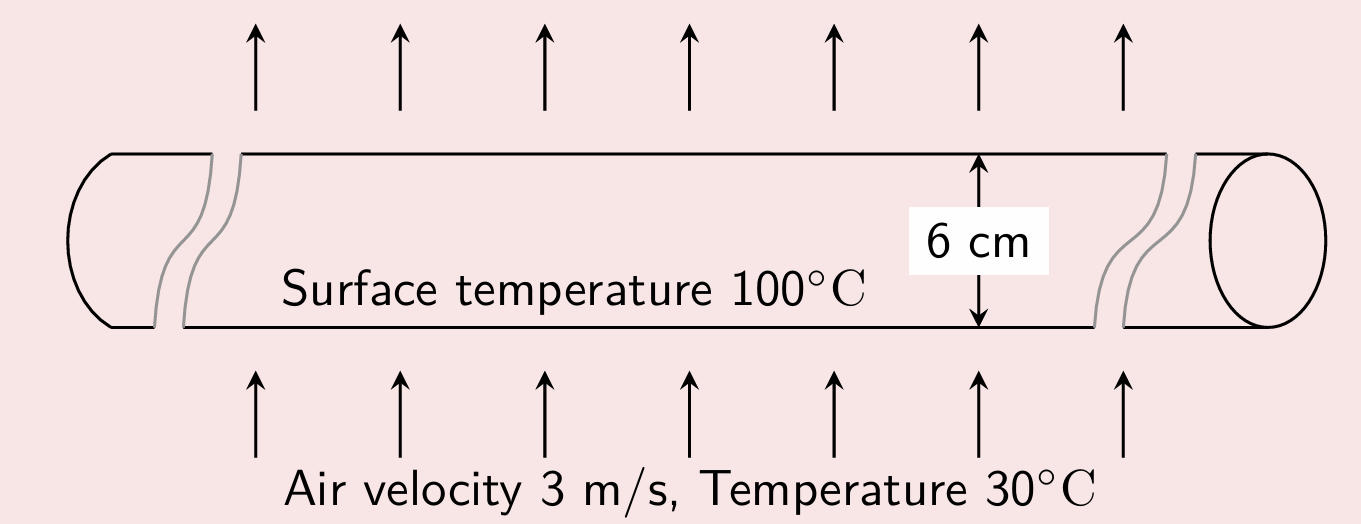
Example 3:Heat Transfer
Rate Air is flowing at a velocity of 3 m/s perpendicular to a
long pipe as shown in the figure below. The outside diameter of the pipe
is \(d=6\) cm and temperature at the
outside surface of the pipe is maintained at 100oC. The temperature of the
air far from the tube is 30oC.
Data for air: Kinematic viscosity, \(\nu=18\times10^{-6}\) m\(^2\)/s;
Thermal conductivity, \(k=0.03\)
W/(m.K)
Using the Nusselt number correlation: \(\text{Nu}=\frac{hD}{k}=0.024\times\text{Re}^{0.8}\), the rate of heat loss per unit length (W/m) from the pipe to air (up to one decimal place) is (GATE-2015-50)
Solution: \[\begin{aligned} \text{Re} &= Dv\rho/mu = Dv/(\mu/\rho) = Dv/\nu \\ &= 6\times10^{-2}\times3/(18\times10^{-6}) = 10000 \\ \text{Nu} &= 0.024\times\text{Re}^{0.8} = 0.024\times(10000)^{0.8} = 38.037 = \frac{hD}{k}\\ h &= 38.037\times \frac{k}{D} = 38.037\times\frac{0.03}{6\times10^{-2}} = 19.02 \text{ W/m$^2$.K} \\ Q &= hA\Delta T = h(\pi DL)\Delta T \\ Q/L &= h(\pi D) \Delta T \\ &= 19.02 \times \pi \times 6\times 10^{-2} \times (100-30) = 251 \text{ W/m} \end{aligned}\]
