31 - Condensation

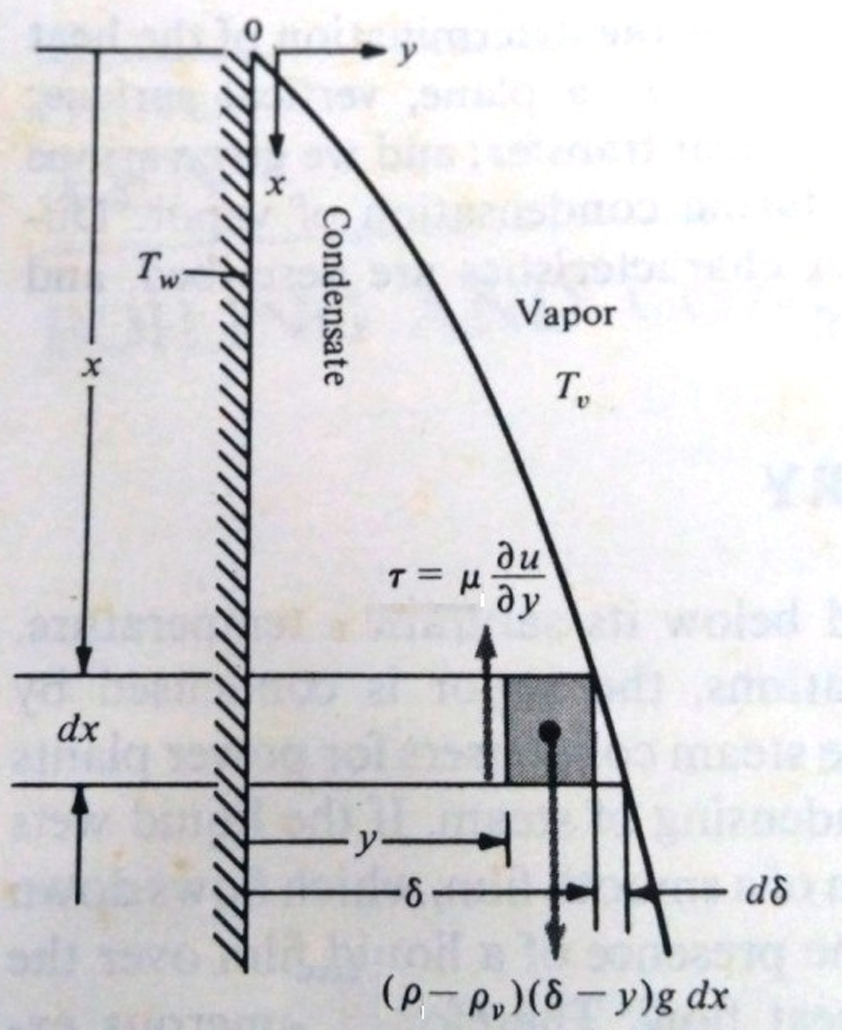
By force balance, shear force acting upward due to flow of fluid in the downward direction is equal to the net gravitational force. \[\tau\; dx = (\rho-\rho_v)(\delta-y)dx\; g\] Using Newton’s law of viscosity, \[\mu\frac{du}{dy}\; dx = (\rho-\rho_v)(\delta-y)g\; dx\] At the wall surface, the liquid velocity is zero: \[u=0 \qquad \text{at }y=0\] Using this, and integrating the above, we get \[u(y) = \frac{g(\rho-\rho_v)}{\mu}\left(\delta y - \frac{1}{2}y^2\right)\] where \(\delta\) is the film thickness at any \(x\).

By definition, mass flow rate = density \(\times\) volumetric flow rate. Therefore, for a unit width of plate, mass flow rate \(m(x)\) through the position \(x\) is \[m(x) = \int_0^{\delta}\rho \, {udy}\] We know, \[u(y) = \frac{g(\rho-\rho_v)}{\mu}\left(\delta y - \frac{1}{2}y^2\right)\] Therefore, \[\begin{aligned} m(x) &= \int_0^{\delta} \rho \frac{g(\rho-\rho_v)}{\mu}\left(\delta y - \frac{1}{2}y^2\right) dy \\ &= \frac{\rho g(\rho-\rho_v)}{\mu}\left[\frac{\delta y^2}{2} - \frac{1}{6}y^3 \right]_0^{\delta} \\ &= \frac{\rho g(\rho-\rho_v)}{\mu}\left[\frac{\delta\cdot\delta^2}{2} - \frac{1}{6}\delta^3 \right] = \frac{\rho g(\rho-\rho_v)}{\mu}\left[\frac{\delta^3}{2} - \frac{\delta^3}{6} \right] \\ \Longrightarrow \qquad m(x)&= \frac{\rho g(\rho-\rho_v)\delta^3}{3\mu} \end{aligned}\]

Differentiating the above, with respect to \(\delta\), we get \[\begin{aligned} \frac{dm}{d\delta} &= \frac{3\rho g(\rho-\rho_v)\delta^2}{3\mu} = \frac{\rho g(\rho-\rho_v)\delta^2}{\mu} \label{dmbyddeltaeqn} \end{aligned}\] The rate of heat transfer (\(dQ_{\text{conden}}\)) associated with rate of condensation \(dm\) is given by \[dQ_{\text{conden}} = \lambda \, dm\] For a film of unit width, and thickness \(dx\), the rate of transfer by conduction(\(dQ_{\text{conduct}}\)), through the film is given by \[dQ_{\text{conduct}} = k\frac{T_v-T_w}{\delta} dx\]

Since, rate of condensation of vapor is equal to the rate of conduction inside the condensate film, we get \[\begin{aligned} dQ = dQ_{\text{conden}} &= dQ_{\text{conduct}} \nonumber \\ \Longrightarrow \quad \lambda \, dm &= k\frac{T_v-T_w}{\delta} dx \nonumber \\ \frac{dm}{dx} &= k\frac{T_v-T_w}{\delta} \label{dmbydxeqn} \end{aligned}\] Eqn.[1] / Eqn.[2] gives \[\frac{d\delta}{dx} = \frac{\mu k(T_v-T_w)}{g\rho(\rho-\rho_v)\lambda}\frac{1}{\delta^3} \tag*{(3)}\] Integrating Eqn.(3), with the condition \(\delta=0\) for \(x=0\) gives, \[\delta(x) = \left[\frac{4\mu k(T_v-T_w)x}{g\rho(\rho-\rho_v)\lambda}\right]^{1/4} \tag*{(4)}\]

Since, we have established the relation for the thickness of the condensate layer, the local heat transfer coefficient \(h_x\), for condensation is determined from the definition: \[\begin{aligned} h_x(T_v-T_w) &= k\frac{T_v-T_w}{\delta(x)} \\ h_x &= \frac{k}{\delta(x)} \end{aligned}\] Using Eqn.(4) in above, we get \[h_x = \left[\frac{g\rho(\rho-\rho_v)\lambda k^3}{4\mu (T_v-T_w)x}\right]^{1/4} \tag*{(5)}\] From the above expression, we could note that the local heat transfer coefficient \(h_x\) varies with the distance as \(x^{-1/4}\). The average heat transfer coefficient \(h_m\) is given by \[h_m = \frac{1}{L}\int_0^L h_x\; dx= \frac{4}{3}h_x\Big|_{L} \tag*{(5)}\]

Using Eqn.(4) in (5) we get, \[\boxed{h_m = 0.943\left[\frac{g\rho(\rho-\rho_v)\lambda k^3}{\mu (T_v-T_w)L}\right]^{1/4} }\] In the above equation \(\rho, \mu\) and \(k\) are properties of liquid.

For using the above equation for inclined plates, \(g\) is replaced by \(g\cos\theta\), where \(\theta\) is the angle between the vertical and the surface. However, it must be used with caution for larger values of \(\theta\) and does not apply if \(\theta=90^\circ\). The expression may be used for condensation on the inner or outer surface a vertical tube of radius \(R\), if \(R\gg\delta\).

The physical properties in the above equation including \(\lambda\) are evaluated at the film temperature \(T_f\) \[T_f = \frac{T_w+T_v}{2}\]