41 - Radiation

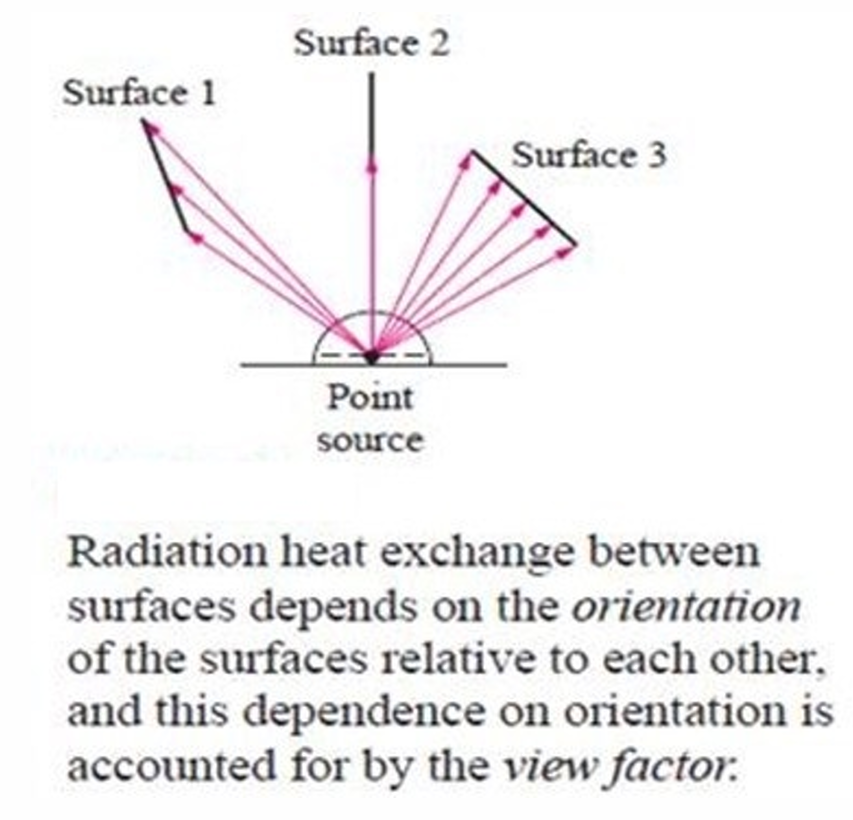
Definition :

View factor (\(F_{ij}\)) is defined as the fraction of the radiation leaving surface \(i\) that is intercepted by \(j\). View factor is also called as shape factor, angle factor, or configuration factor.

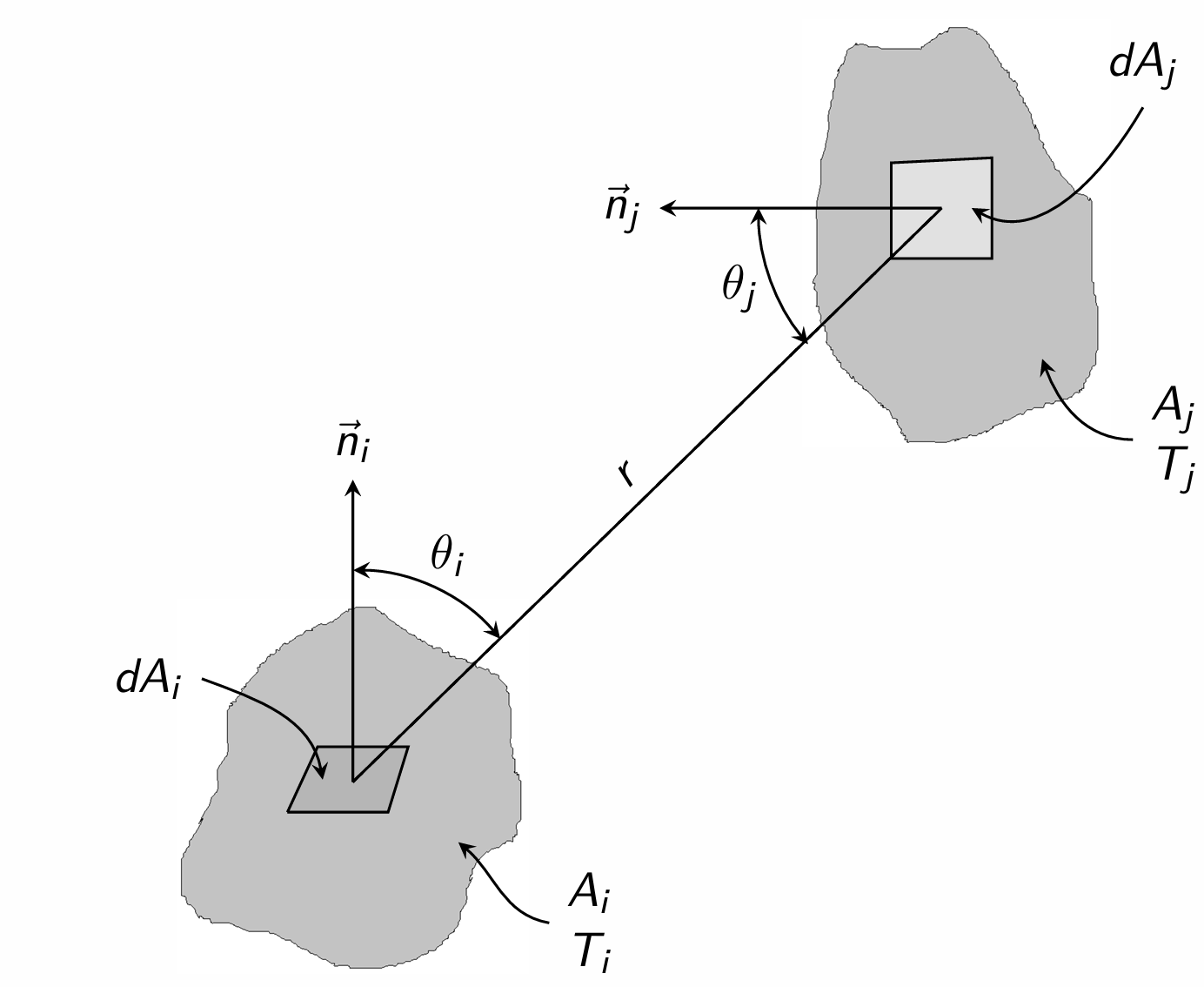
View factor from \(A_1\) to \(A_2\) is obtained by \[F_{A_1\text{--}A_2} = \frac{1}{A_1}\int_{A_1}\int_{A_2}\frac{\cos\theta_1\; \cos\theta_2}{\pi r^2}dA_2\;dA_1\] View factor from \(A_2\) to \(A_1\) is obtained by \[F_{A_2\text{--}A_1} = \frac{1}{A_2}\int_{A_2}\int_{A_1}\frac{\cos\theta_1\; \cos\theta_2}{\pi r^2}dA_1\;dA_2\]

• Reciprocity relation: \[A_iF_{ij} = A_jF_{ji}\]

• Summation rule: \[\sum_j F_{ij} = 1\] For exchange between two surfaces, \(F_{11} + F_{12} = 1\), and \(F_{21} + F_{22} = 1\)

• \(F_{ii}\) is the view factor from the surface \(A_i\) to itself.

  \(F_{ii} = 0\), for a convex or flat surface. \(F_{ii} \ne 0\), if \(A_i\) is concave.