42 - Evaporation
10. Solved Problems
Example 1: Evaporator A solution containing 10% of solids is to be concentrated to a level of 50% solids. Steam is available at a pressure of 0.2 MPa (saturation temperature of 393 K). Feed rate to the evaporator is 30000 kg/hr. The evaporator is operating at a reduced pressure such that the boiling point is 323 K. The overall heat transfer coefficient is 2.9 kW/m\(^2\).K. Estimate (i) The steam economy, and (ii) The heat transfer surface for (1) Feed introduced at 293 K, (2) Feed introduced at 308 K. (AU-Nov-2014)
Data:
Specific heat of feed = 3.98 kJ/kg.K
Latent heat of condensation of steam at 0.2 MPa = 2202 kJ/kg
Latent heat of vaporization of water at 323 K = 2383 kJ/kg
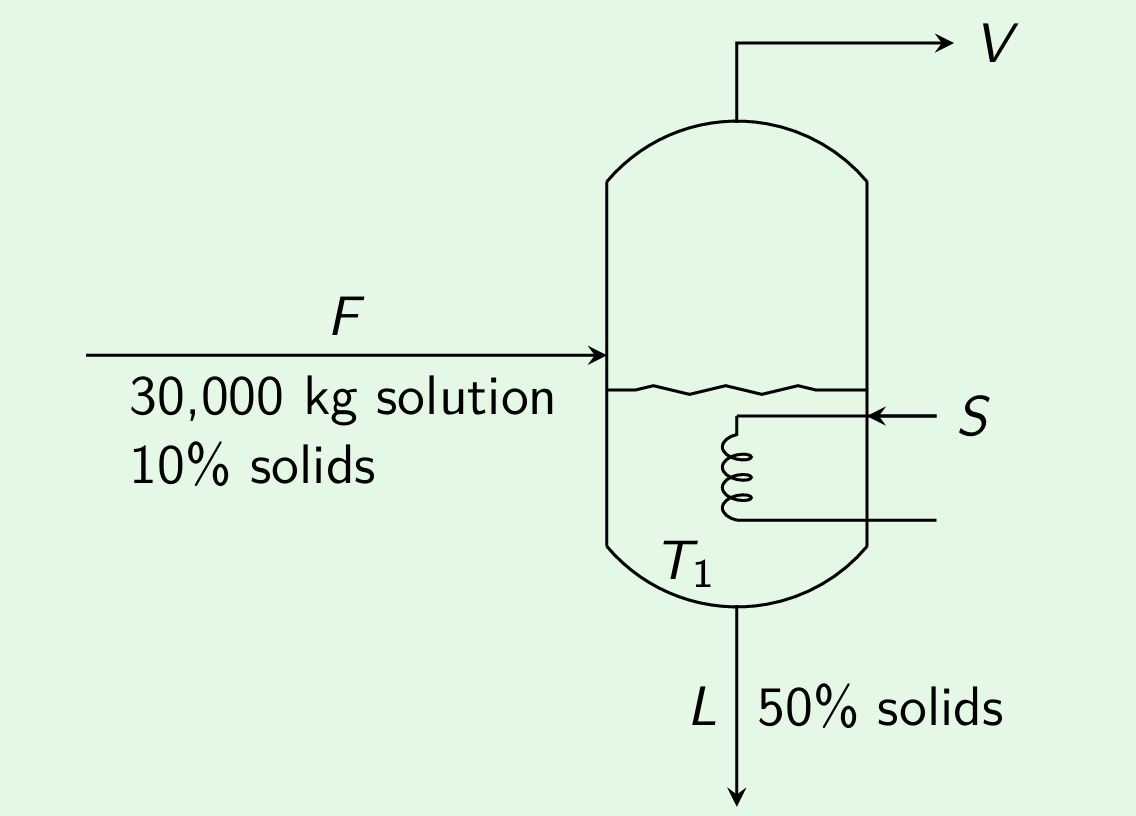
Mass balance: \[\begin{align*} \text{Overall balance:} \\ F &= L + V \\ 30000 = L + V \tag*{(1)} \\ \text{Solute balance:} \\ Fx_F &= Lx_L \\ 30000\times0.1 &= L\times0.5 \\ L &= 6000 \text{ kg/hr} \\ \text{Using the above in Eqn.(1), we get} \\ V &= 30000 - 6000 = 24000 \text{ kg/hr} \end{align*}\]
Feed temperature = 293 K
Energy balance: By choosing the reference temperature as boiling point of solution (\(T_1\)), we get \[\begin{aligned} S\lambda_S &= V\lambda_V + FC_P(T_1-T_F) \\ S\times2202&=24000\times2383 + 30000\times3.98\times(323-293) \\ S &= 27,708.4 \text{ kg/hr} \\ \text{Economy} &= \frac{V}{S} = \frac{24000}{27708.4} = 0.87 \\ \text{Heat transfer area} (A) &= \frac{Q}{U\;\Delta T_m} \\ &= \frac{S\lambda_S}{U\;(T_S-T_1)} = \frac{(27708.4/3600)\times2202}{2.9\times(393-323)} \\ &= 83.5 \text{ m$^2$} \end{aligned}\]
Feed temperature = 308 K
By similar calculations, we get \(S=26,786.1\) kg/hr, and, \[\text{Economy} = 0.896 \qquad \text{Heat transfer area} =80.7 \text{ m$^2$}\]
Because of the increase in feed temperature, steam economy increased, and required area for heat transfer got reduced.
