17-Heat Exchangers - LMTD Method
2. LMTD for Heat Exchanger Analysis
Cocurrent Flow
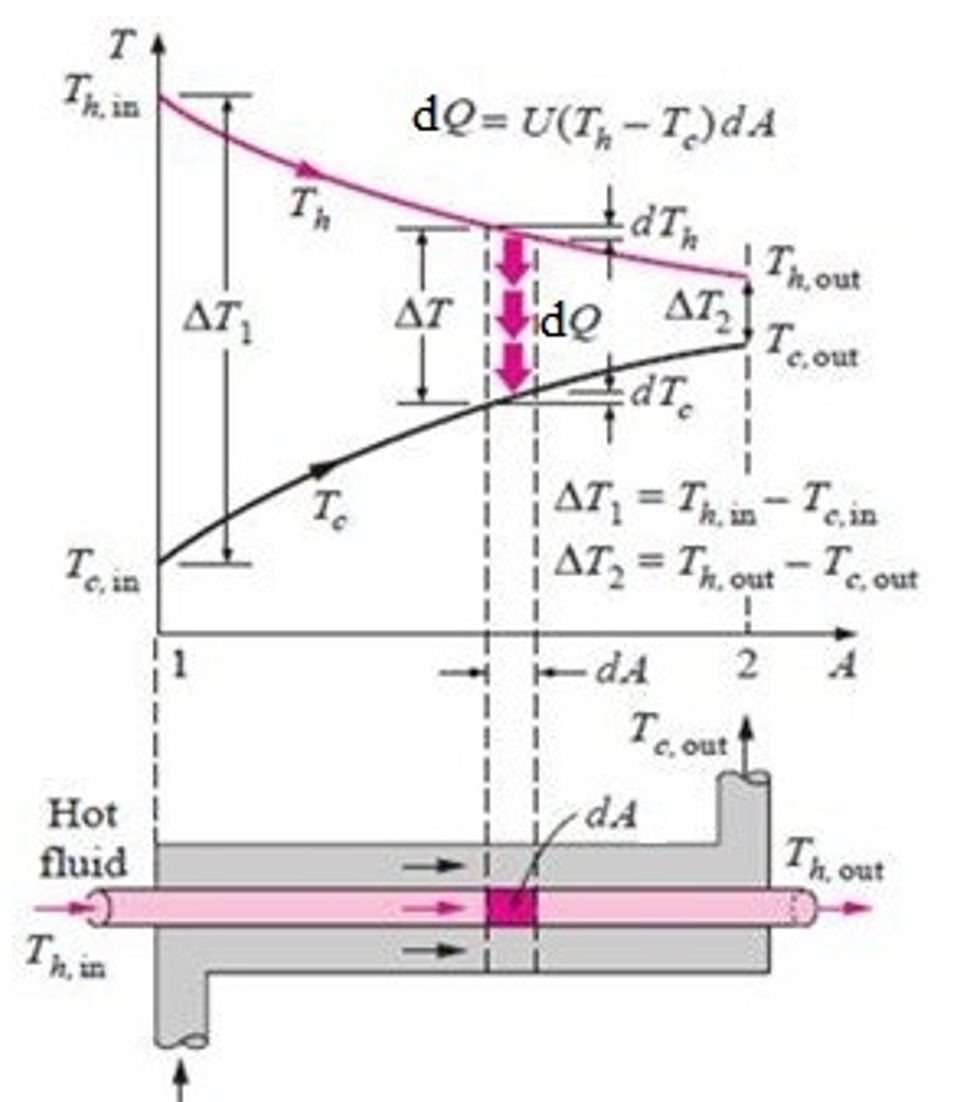
\[Q = UA \Delta T_m \tag*{(1)}\] For an elemental area \(dA\), \[dQ = U (\Delta T) (dA) \tag*{(2)}\] where \(\Delta T = T_h-T_c\)
From heat capacity relations, for the cold and hot fluids, we have \[\begin{align*} dQ &= \dot{m_c}C_{P,c}\;dT_c = C_c\; dT_c \tag*{(3a)} \\ dQ &= -\dot{m_h}C_{P,h}\;dT_h = -C_h\; dT_h \tag*{(3b)} \end{align*}\] where \(C_c=\dot{m_c}C_{P,c}\), and \(C_h=\dot{m_h}C_{P,h}\)
\[\begin{aligned} \Delta T &= T_h - T_c \\ d(\Delta T) &= dT_h - dT_c\\ \text{Substituting for $dT_h$ and $dT_c$ from Eqn.(3), we get} \\ d(\Delta T)&= -\frac{dQ}{C_h} - \frac{dQ}{C_c} = -dQ\left(\frac{1}{C_h} + \frac{1}{C_c} \right) \end{aligned}\] Substituting for \(dQ\) from Eqn.(2), we get \[d(\Delta T) = -U (\Delta T) (dA)\left(\frac{1}{C_h} + \frac{1}{C_c} \right)\] Rearranging, \[\frac{d(\Delta T)}{\Delta T} = -U (dA)\left(\frac{1}{C_h} + \frac{1}{C_c} \right)\]
For constant \(U\), \[\begin{align*} \int_{\Delta T_1}^{\Delta T_2}\frac{d(\Delta T)}{\Delta T} &= -U\left(\frac{1}{C_h} + \frac{1}{C_c} \right) \int_0^A dA \\ \ln \frac{\Delta T_2}{\Delta T_1} &= -UA\left(\frac{1}{C_h} + \frac{1}{C_c} \right) \tag*{(4)} \end{align*}\] For the cold and hot fluids, we have \[\begin{align*} Q &= C_c(T_{c,\text{out}}-T_{c,\text{in}}) = C_c(T_{c2}-T_{c1}) \\ Q &= C_h(T_{h,\text{in}}-T_{h,\text{out}}) = C_h(T_{h1}-T_{h2}) \end{align*}\] From these we get \[\begin{align*} \frac{1}{C_c} &= \frac{T_{c2}-T_{c1}}{Q} \tag*{(5a)} \\ \frac{1}{C_h} &= \frac{T_{h1}-T_{h2}}{Q} \tag*{(5b)} \end{align*}\]
