2. Effectiveness - NTU Method

In order to use this method we need three new definitions:

  • Thermal Capacity Ratio (\(C\)):

    The thermal capacity of a fluid stream is the quantity of heat it can transport per unit change in temperature:
    i.e. its mass flow \(\times\) specific heat capacity. \[C = \frac{(\dot{m}C_P)_{\text{min}}}{(\dot{m}C_P)_{\text{max}}} = \frac{C_{\text{min}}}{C_{\text{max}}}\]

  • Thermal Effectiveness (\(\varepsilon\)): \[\begin{aligned} \varepsilon &= \frac{\text{actual heat transfer rate}}{\text{theoretical maximum heat transfer rate}} \\ &= \frac{Q}{Q_{\text{max}}} = \frac{Q}{C_{\text{min}}(T_{hi}-T_{ci})} \end{aligned}\] The maximum theoretical heat transfer rate occurs in counterflow with infinite heat transfer surface area. It cannot occur in parallel flow because the exit temperature must be between the two inlet temperatures.

Maximum Possible Heat Transfer:


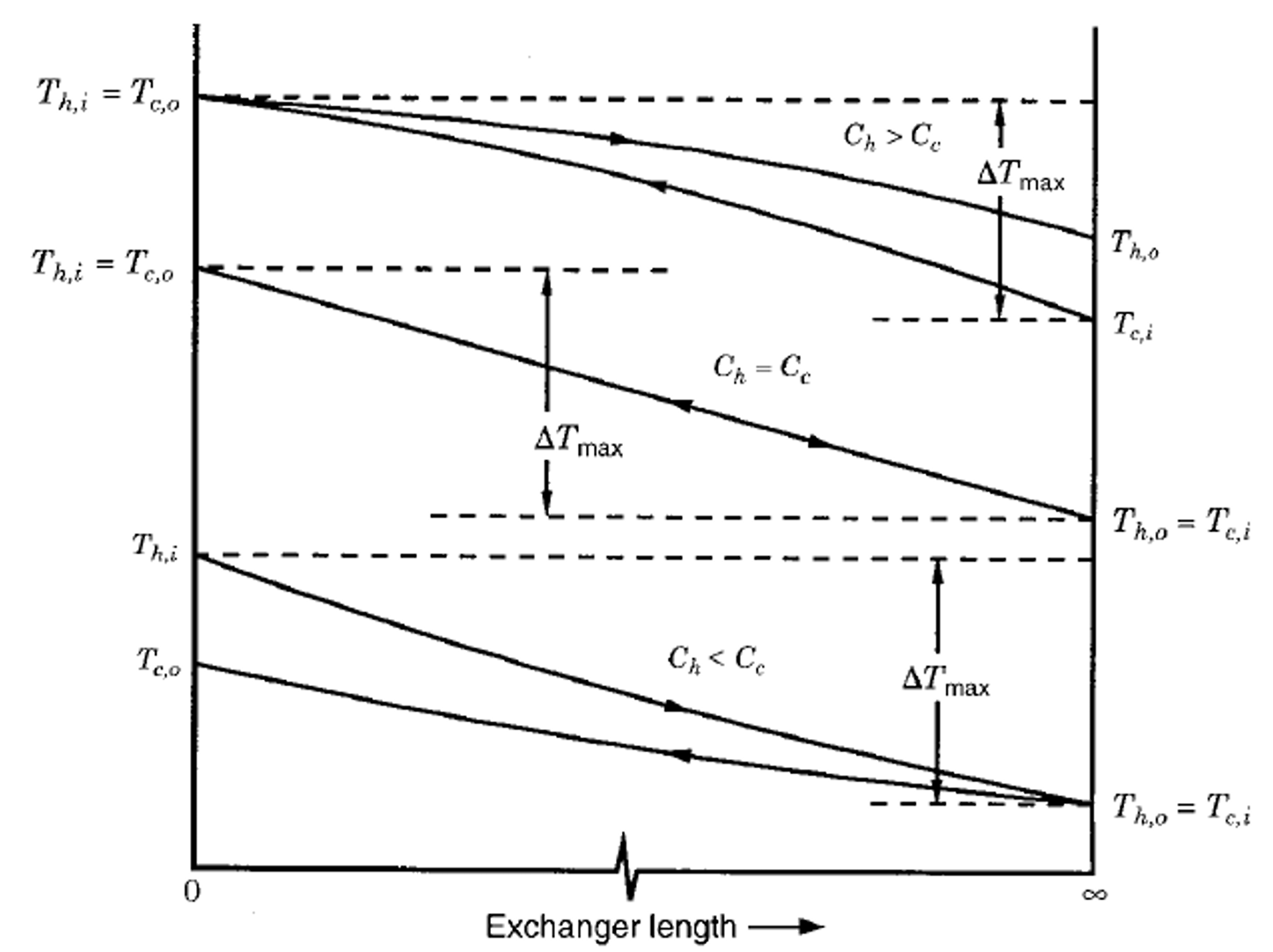
The maximum theoretical heat transfer is given by: \[Q_{\text{max}} = (\dot{m}C_P)_{\text{min}}(T_{hi}-T_{ci}) = C_{\text{min}}(T_{hi}-T_{ci})\] The actual heat transfer rate is given by: \[\begin{aligned} Q &= (\dot{m}C_P)_h (T_{hi}-T_{ho}) = C_h(T_{hi}-T_{ho}) \\ &= (\dot{m}C_P)_c (T_{co}-T_{ci}) = C_c (T_{co}-T_{ci}) \end{aligned}\]

  • Number of Transfer Units (NTU): \[\text{NTU} = \frac{UA}{(mC_P)_{\text{min}}} = \frac{UA}{C_{\text{min}}}\]