52 - Heat Exchangers - Effectiveness-NTU Method
7. Solved Problems
Example 2: The Lowest Possible Temperature in a Parallel Flow Exchanger The engine oil at 150oC is cooled to 80oC in a parallel flow heat exchanger by water entering at 25oC and leaving at 60oC. Estimate the exchanger effectiveness and the number of transfer units. If the fluid flow rates and inlet conditions remain unchanged, work out the lowest temperature to which the oil may be cooled by increasing the length of the exchanger. (AU-Nov-2016)
Solution:
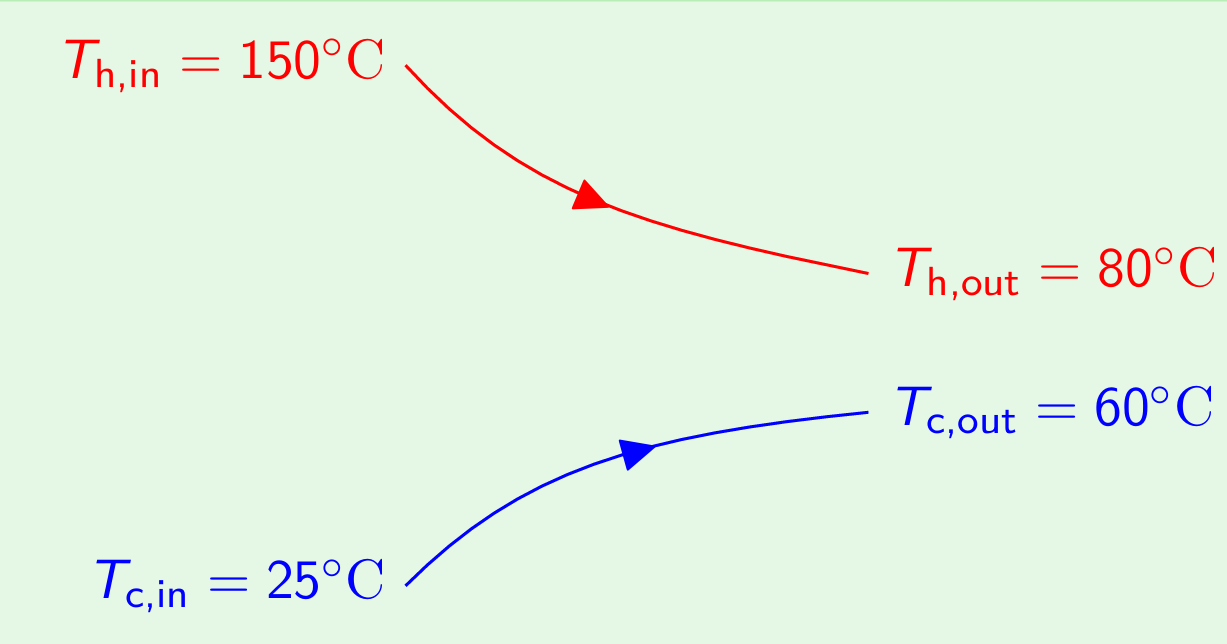
Effectiveness (\(\varepsilon\)): \[\varepsilon = \frac{Q}{Q_{\text{max}}} = \frac{Q}{C_{\text{min}}(T_{\text{h,in}}-T_{\text{c,in}})} = \frac{Q}{C_{\text{min}}(150-25)} \tag*{(1)}\] To find the value of \(\varepsilon\) from the above equation, we need to find the fluid which is having \(C_{\text{min}}\), and use the expression of \(Q=C_{\text{min}}\Delta T_{\text{max}}\) From energy balance between the fluids, \[Q =C_{\text{min}}\Delta T_{\text{max}} = C_{\text{max}} \Delta T_{\text{min}} \tag*{(2)}\] From the data given \[\begin{aligned} \Delta T_{\text{oil}} &= 150 - 80 = 70^\circ\text{C} \\ \Delta T_{\text{water}} &= 60 - 25 = 35^\circ\text{C} \end{aligned}\] \(\Delta T\) is higher for oil. Therefore, \(C_{\text{min}}=C_{\text{oil}}\), and \(C_{\text{max}}=C_{\text{water}}\)
Hence, Eqn.(2) becomes, \[Q =C_{\text{min}}(150-80)= C_{\text{max}}(60-25) \tag*{(3)}\] Using Eqn.(3), in Eqn.(1), we get \[\varepsilon = \frac{C_{\text{min}}(150-80)}{C_{\text{min}}(150-25)} = 0.56\]
Heat capacity ratio (\(C\)): \[C = \frac{C_{\text{min}}}{C_{\text{max}}} \tag*{(4)}\] From Eqn.(3), we have \[\frac{C_{\text{min}}}{C_{\text{max}}} = \frac{60-25}{150-80}=0.5 = \frac{C_{\text{oil}}}{C_{\text{water}}} \tag*{(5)}\]
Number of Transfer Units (\(N\)): \[N = \frac{UA}{C_{\text{min}}}\] From the definition of effectiveness, we have \[\varepsilon = \frac{Q}{C_{\text{min}}(T_{\text{h,in}}-T_{\text{c,in}})} = \frac{UA\;\Delta T_{\text{lm}}}{C_{\text{min}}(T_{\text{h,in}}-T_{\text{c,in}})} = N \frac{\Delta T_{\text{lm}}}{(T_{\text{h,in}}-T_{\text{c,in}})}\] For the given parallel flow exchanger, \[\Delta T_{\text{lm}} = \frac{(150-25)-(80-60)}{\ln[(150-25)/(80-60)]} = 57.3^{\circ}C\] Hence, \[N = \varepsilon \frac{T_{\text{h,in}}-T_{\text{c,in}}}{\Delta T_{\text{lm}}} = 0.56\times\frac{150-25}{57.3} =1.22\]
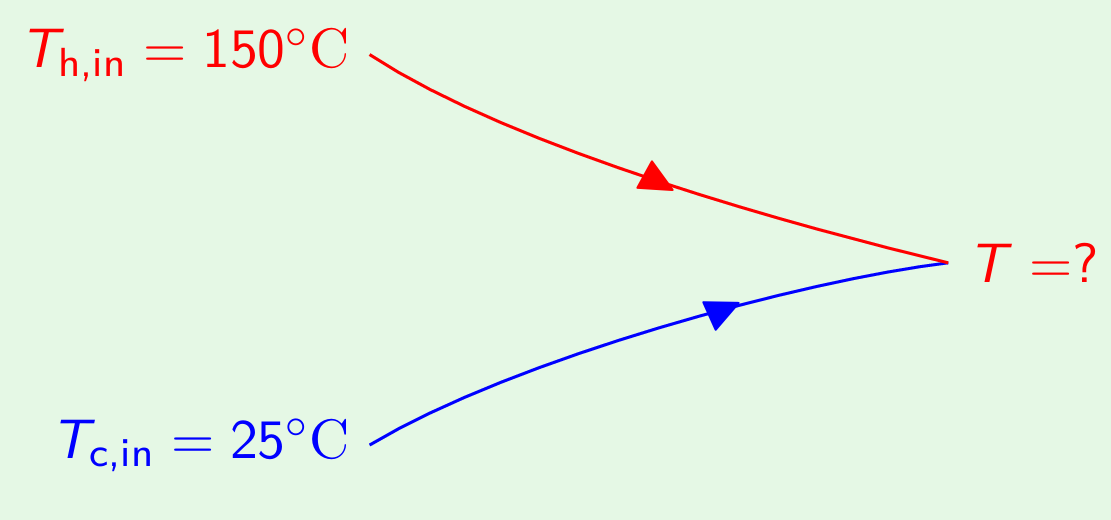
From energy balance, \[C_{\text{oil}}(150-T) = C_{\text{water}}(T-25) \qquad \Longrightarrow \quad \frac{150-T}{T-25} = \frac{C_{water}}{C_{oil}}\] Using Eqn.(5) in above, we get \[\frac{150-T}{T-25} = \frac{1}{0.5}\]
Solved Problems (contd..)
i.e., \[0.5\times(150-T) = T-25 \qquad \Longrightarrow \quad T = 66.7^{\circ}C\] Extension of the problem:
With infinite heat transfer area, if the arrangement were countercurrent, then oil (the fluid with \(C_{\text{min}}\)) will exit at the temperature of 25oC.
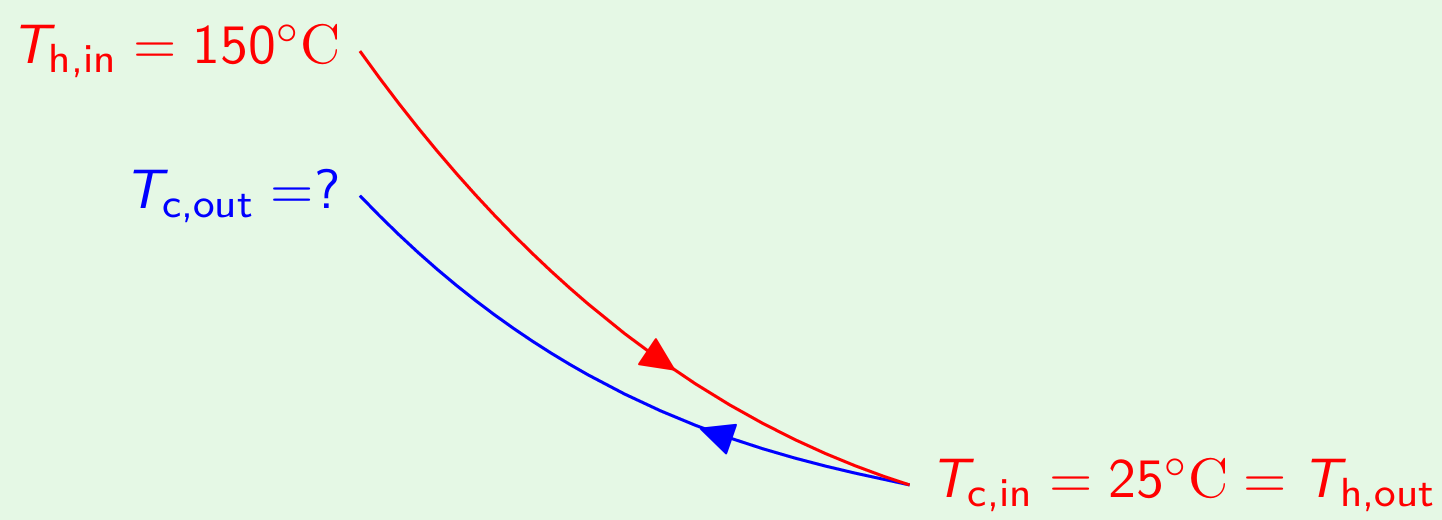
The exit temperature of water (\(T_{\text{c,out}}\)) is obtained as below: \[C_{\text{water}}(T_{\text{c,out}}-25) = C_{\text{oil}}(150-25) \qquad \frac{T_{\text{c,out}}-25}{150-25} = \frac{C_{\text{oil}}}{C_{\text{water}}}\] From the previous calculations, we have \[\frac{C_{\text{oil}}}{C_{\text{water}}} = 0.5\] hence, \[\frac{T_{\text{c,out}}-25}{150-25} = 0.5 \qquad \Longrightarrow \quad T_{\text{c,out}} = 87.5\]
