7. First Order System - Response to Step Input

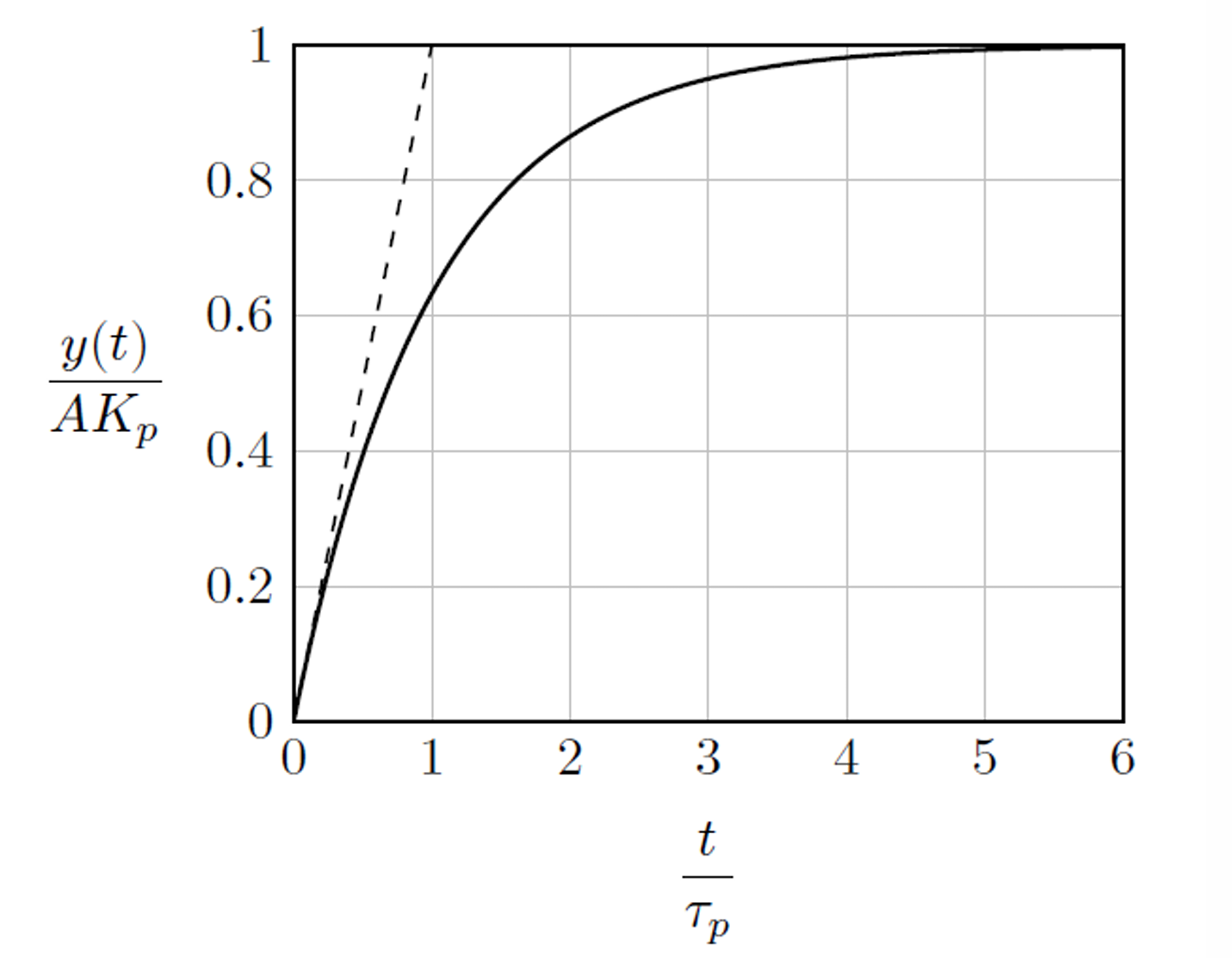
The transfer function of first order system is given by \[G(s) = \frac{Y(s)}{X(s)} = \frac{K_p}{\tau_p s + 1}\] Let us examine how it responds to a unit step change in input, \(x(t)\).

For unit step input, \(X(s)=\dfrac{1}{s}\). Therefore, \[Y(s) = \frac{K_p}{s(\tau_p s+1)} = \frac{K_p}{s} - \frac{K_p\tau_p}{\tau_ps+1}\] Taking inverse Laplace transform, we get \[y(t) = K_p(1-e^{-t/\tau_p})\] For step input of magnitude \(A\), \[y(t) = AK_p(1-e^{-t/\tau_p})\]