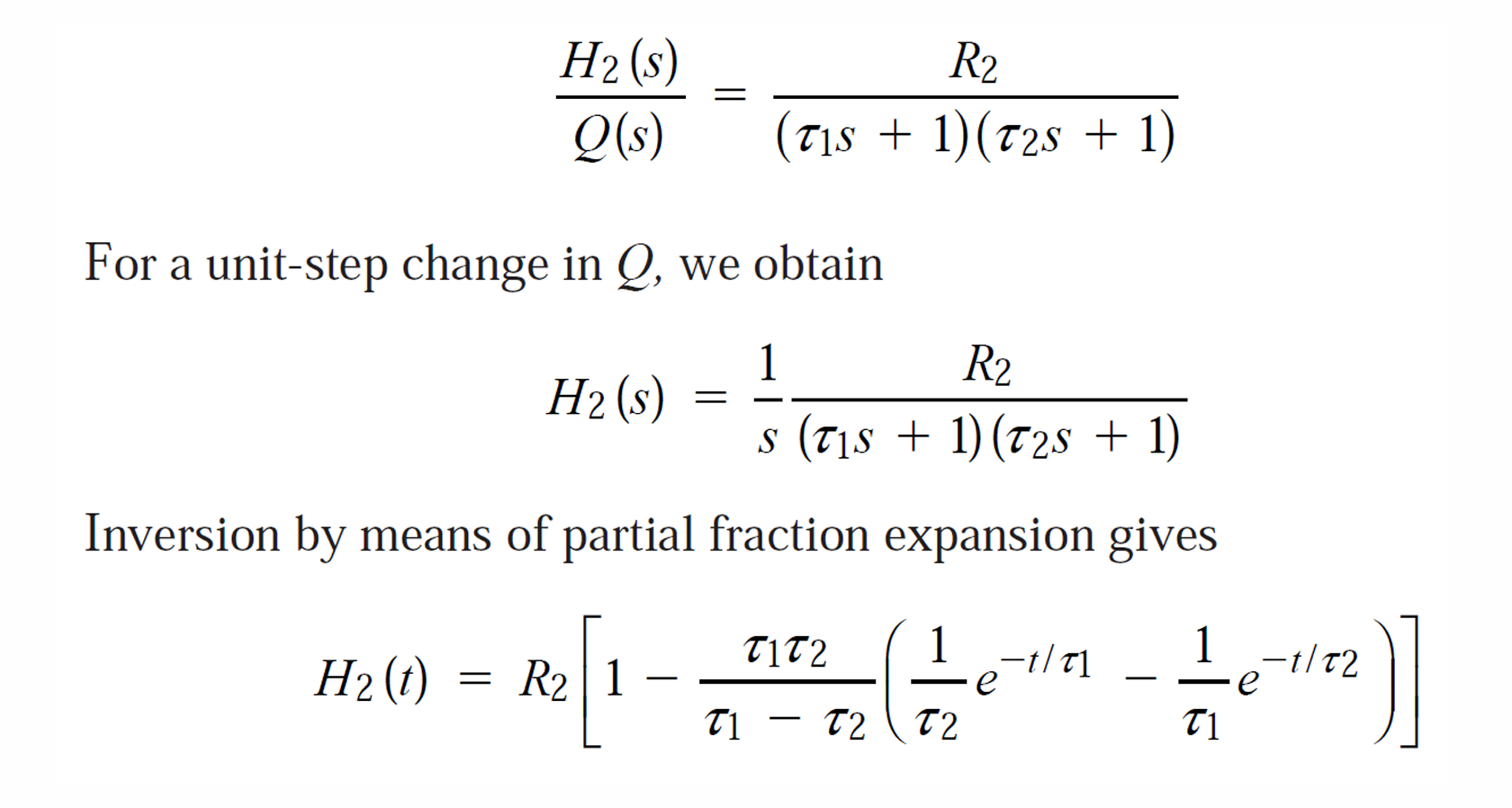03 - First Order Systems in Series

Tank-1:

Material balance: \[q - q_1 = A_1\frac{dh_1}{dt} \label{eqnNoninteract1}\] Relation between \(q_1\) and \(h_1\): \[q_1 = \frac{h_1}{R_1} \label{eqnNoninteract2}\] Tank-2:

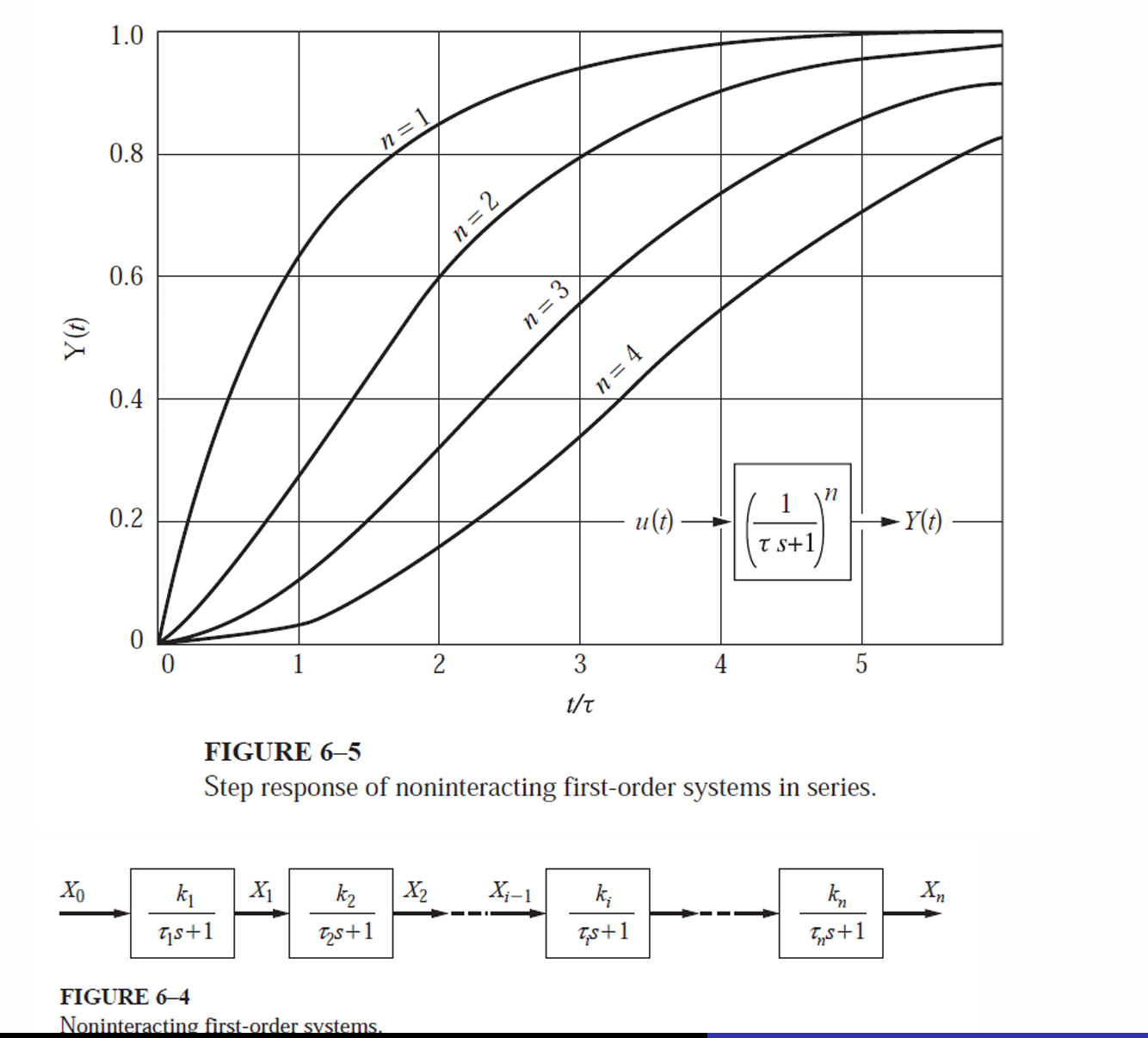
Material balance: \[q_1 - q_2 = A_2\frac{dh_2}{dt} \label{eqnNoninteract3}\] Relation between \(q_2\) and \(h_2\): \[q_2 = \frac{h_2}{R_2} \label{eqnNoninteract4}\] Writing the above equations in deviation variables {<span class="math inline">\(Q=q-q_s; Q_1 = q_1 - q_{1s} \ H_1 = h_1-h_{1s}; \ H_2 = h_2-h_{2s}\) }, taking Laplace transforms, and using \(A_1R_1=\tau_1; \ A_2R_2=\tau_2\), we get

\[\begin{aligned} \frac{H_1(s)}{Q(s)} &= \frac{R_1}{\tau_1s +1} \label{eqnNoninteract5} \\ \frac{Q_1(s)}{Q(s)} &= \frac{1}{\tau_1s +1} \label{eqnNoninteract6} \\ \frac{H_2(s)}{Q_1(s)} &= \frac{R_2}{\tau_2s +1} \label{eqnNoninteract7} \shortintertext{And,} \frac{H_2(s)}{Q(s)} &= \frac{1}{\tau_1s +1}\frac{R_2}{\tau_2s +1} \label{eqnNoninteract8} \\ \frac{Q_2(s)}{Q(s)} &= \frac{1}{\tau_1s +1}\frac{1}{\tau_2s +1} \label{eqnNoninteract9} \end{aligned}\] Eqn.[eqnNoninteract9] can be generalized for multiple (non-interacting) systems in series as \[\frac{Q_N(s)}{Q(s)} = \frac{K_{p1}}{\tau_1s +1}\frac{K_{p2}}{\tau_2s +1} \cdots \frac{K_{pN}}{\tau_Ns +1}\]