04 - Second Order Systems

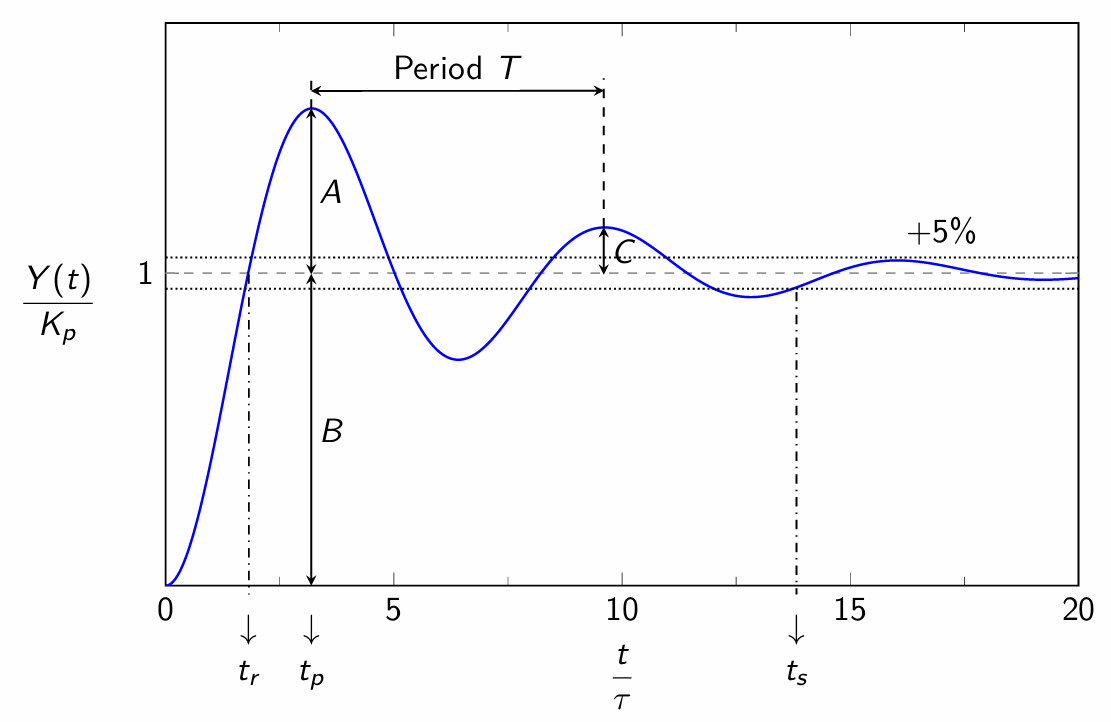
This is the most commonly exhibited behavior with second order systems.

Rise time (\(t_r\)): It is the time the process output takes to first reach the new steady-state value.

Peak time (\(t_p\)): It is the time for the first peak to appear from the start of response. \[t_p = \frac{\pi \tau}{\sqrt{1-\zeta^2}}\]

Overshoot: It’s about how much the response exceeds its ultimate value. \[\text{Overshoot } = \frac{A}{B} = \exp\left(\frac{-\pi\zeta}{\sqrt{1-\zeta^2}}\right)\]

Decay ratio: It’s the ratio of successive peaks of the response. \[\text{Decay ratio } = \frac{C}{A} = \text{(Overshoot)}^2 = \exp\left(\frac{-2\pi\zeta}{\sqrt{1-\zeta^2}}\right)\]

Period of oscillation (\(T\)): It is the time elapsed between two successive peaks (or two successive valleys) of the response. \[T = \frac{2\pi\tau}{\sqrt{1-\zeta^2}}\] and \[\omega = 2\pi f = \frac{2\pi}{T}\] Natural cyclical period of oscillation (\(T_n\)) is the period of oscillation at \(\zeta=0\). Hence, \[T_n = 2\pi\tau\]

Settling time (\(t_s\)): It is also known as response time. It is defined as the time required for the response to come within \(\pm5\%\) (or \(\pm2\%\)) of its ultimate value and remain there. It’s value is given as: \[t_s = \dfrac{3\tau}{\zeta} \quad (\text{5% criterion}) \qquad \qquad t_s = \dfrac{4\tau}{\zeta} \quad (\text{2% criterion})\]