04 - Second Order Systems

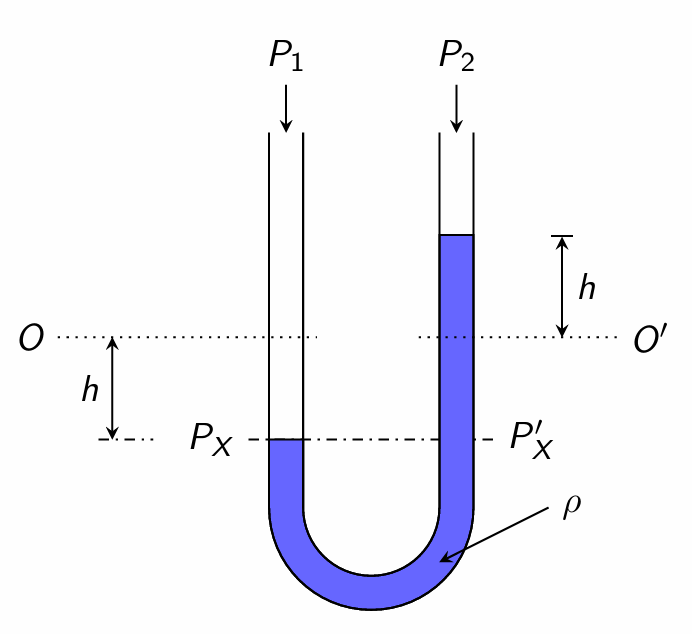
Force balance at plane \(XX\)’: \[P_1A - P_2A - \rho g (2h) A - \left(\begin{array}{c}\text{force due to}\\ \text{fluid friction} \end{array}\right) = m \frac{dv}{dt} \label{eqnMano1}\] Mass of manometric fluid = \(m=\rho AL\).

Velocity of fluid = \(v=\dfrac{dh}{dt}\). Hence, \[\frac{dv}{dt} = \frac{d^2h}{dt^2}\]

Force due to friction = \(\Delta P_f A\).

Assuming laminar flow, \[\Delta P_f = \frac{2fL\rho v^2}{D} = \frac{32\mu L v}{D^2} = \frac{8\mu L}{R^2}\frac{dh}{dt}\]

Substituting for the known quantities, in Eqn.[eqnMano1], we get \[P_1A-P_2A - \rho g(2h)A - \frac{8\mu LA}{R^2}\frac{dh}{dt} = \rho AL\frac{d^2h}{dt^2}\] Dividing by \(2\rho gA\) throughout, and rearranging, we get \[\frac{L}{2g}\frac{d^2h}{dt^2} + \frac{4\mu L}{\rho gR^2}\frac{dh}{dt} + h = \frac{P_1-P_2}{2\rho g}\] i.e., \[\tau^2\frac{d^2h}{dt^2} + 2\tau\zeta\frac{dh}{dt} + h = K_p\Delta P\] where \[\tau^2 = \frac{L}{2g} \qquad 2\tau\zeta =\frac{4\mu L}{\rho gR^2} \qquad K_p = \frac{1}{2\rho g}\]