05 - Closed Loop Systems

Energy balance: (constant density, constant volume, constant flow system) \[FC_P\rho(T_i-T)+Q = V\rho C_P\frac{dT}{dt}\] Heat input by steam is given by \[Q = UA(T_{st}-T)\] Therefore, energy balance equation becomes, \[V\frac{dT}{dt} + \left(F+\frac{UA}{\rho C_P}\right)T = FT_i + \frac{UA}{\rho C_P}T_{st}\] Substituting, \(\dfrac{F}{V}=\dfrac{1}{\tau}\), and \(K=\dfrac{UA}{V\rho C_P}\), and \(a=\dfrac{1}{\tau}+K\), we get \[\frac{dT}{dt} + aT = \frac{1}{\tau}T_i + KT_{st}\]

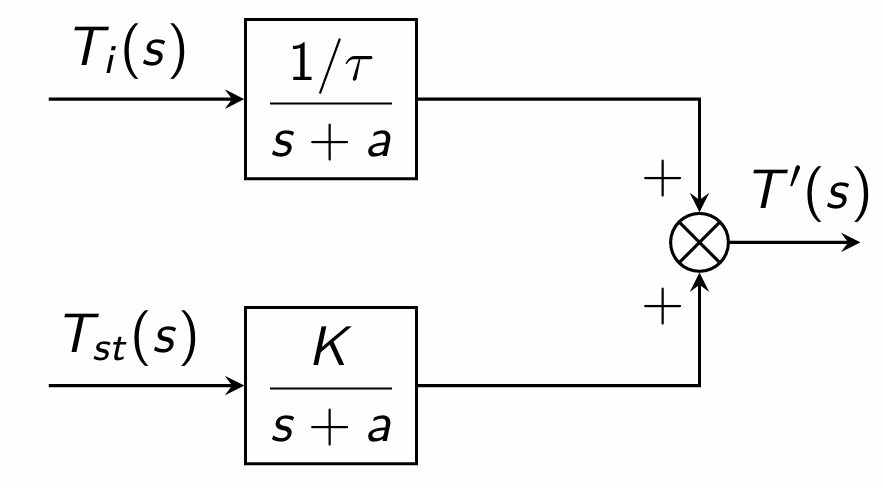
Using deviation variables and taking Laplace transform, we get \[\begin{aligned} (s+a)T'(s) &= \frac{1}{\tau}T'_i(s) + KT'_{st}(s) \\ T'(s) &= \frac{1/\tau}{s+a}T'_i(s) + \frac{K}{s+a}T'_{st}(s) \end{aligned}\]

Block Diagram Representation: