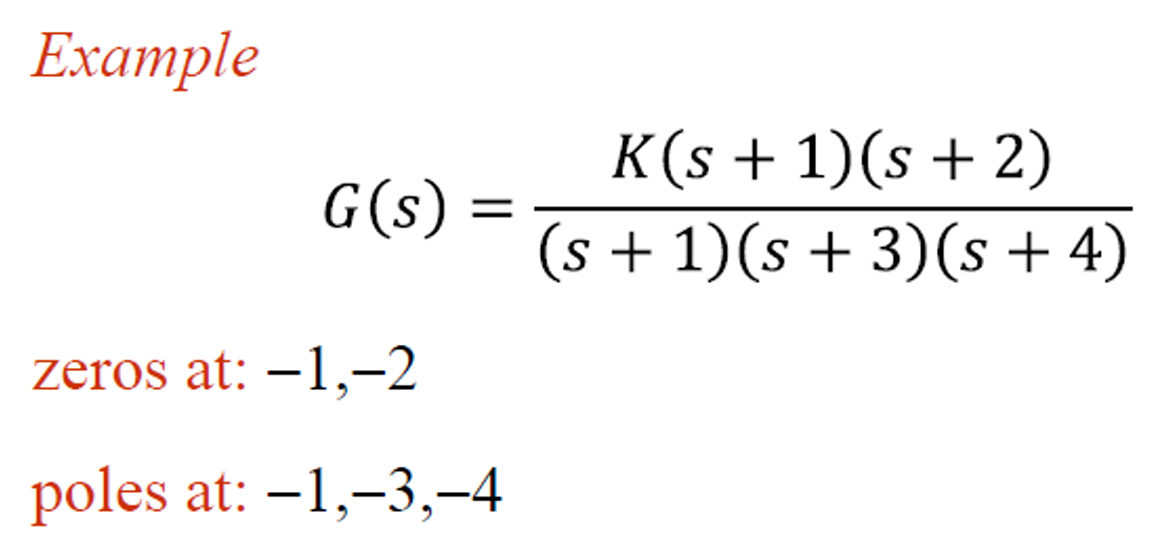08 - Pole Zero Analysis

The above equation (given in previous slide) in pole-zero form is given as \[G(s) = \frac{Q(s)}{P(s)} = K\frac{(s-z_1)(s-z_2)\cdots (s-z_m)}{(s-p_1)(s-p_2)\cdots (s-p_n)}\] where \(p\) are poles and \(z\) are zeros of the transfer function. The zeros affect only the coefficients of the solution \(y(t)\), but not the time dependent functions. Therefore in qualitative discussions, the focus is only on the poles.

Zeros affect the overall shape of the response.

‘Poles’ are values of \(s\) that make the denominator of transfer function zero. Similarly, ‘zeros’ are values of \(s\) that make the numerator of transfer function zero.

At a‘pole’ the transfer function of the system becomes infinite. At a ‘zero’ the transfer function of the system becomes 0.

The poles and zeros are properties of the transfer function, and therefore of the differential equation describing the input-output system dynamics. Together with the gain constant \(K\) they completely characterize the differential equation, and provide a complete description of the system.