11 - Frequency Response

For a first order system, \[G_p(s) = \frac{Y(s)}{X(s)} = \frac{K_p}{\tau_ps+1}\] Let \(X(t)\) be a sinusoidal input with amplitude \(A\) and frequency \(\omega\). \[X(t) = A\sin(\omega t)\] Then, \[X(s) = \frac{A\omega}{s^2+\omega^2}\] Hence, \[Y(s) = \frac{K_p}{\tau_ps+1}\;\frac{A\omega}{s^2+\omega^2} = \frac{C_1}{s+1/\tau_p} + \frac{C_2}{s+j\omega} + \frac{C_3}{s-j\omega}\]

Evaluating the coefficients \(C_1,C_2,C_3\), and taking inverse Laplace transform, we get \[Y(t) = \frac{K_pA\omega\tau_p}{\tau_p^2\omega^2+1}e^{-t/\tau_p} - \frac{K_pA\omega\tau_p}{\tau_p^2\omega^2+1}\cos(\omega t) + \frac{K_pA}{\tau_p^2\omega^2+1}\sin(\omega t)\] As \(t\rightarrow \infty\), \(e^{-t/\tau_p}\rightarrow 0\). Hence, \[Y_{ss}(t) = - \frac{K_pA\omega\tau_p}{\tau_p^2\omega^2+1}\cos(\omega t) + \frac{K_pA}{\tau_p^2\omega^2+1}\sin(\omega t)\] Using the following trigonometric identity in the above: \[a_1\cos b + a_2\sin b = a_3\sin(b+\phi)\] where \[a_3 = \sqrt{a_1^2+a_2^2} \qquad \text{and} \qquad \phi = \tan^{-1}\left(\frac{a_1}{a_2}\right)\]

\[Y_{ss}(t) = \frac{AK_p}{\sqrt{\tau_p^2\omega^2+1}}\sin(\omega t+\phi)\] where \[\phi = \tan^{-1}(-\omega \tau_p)\]

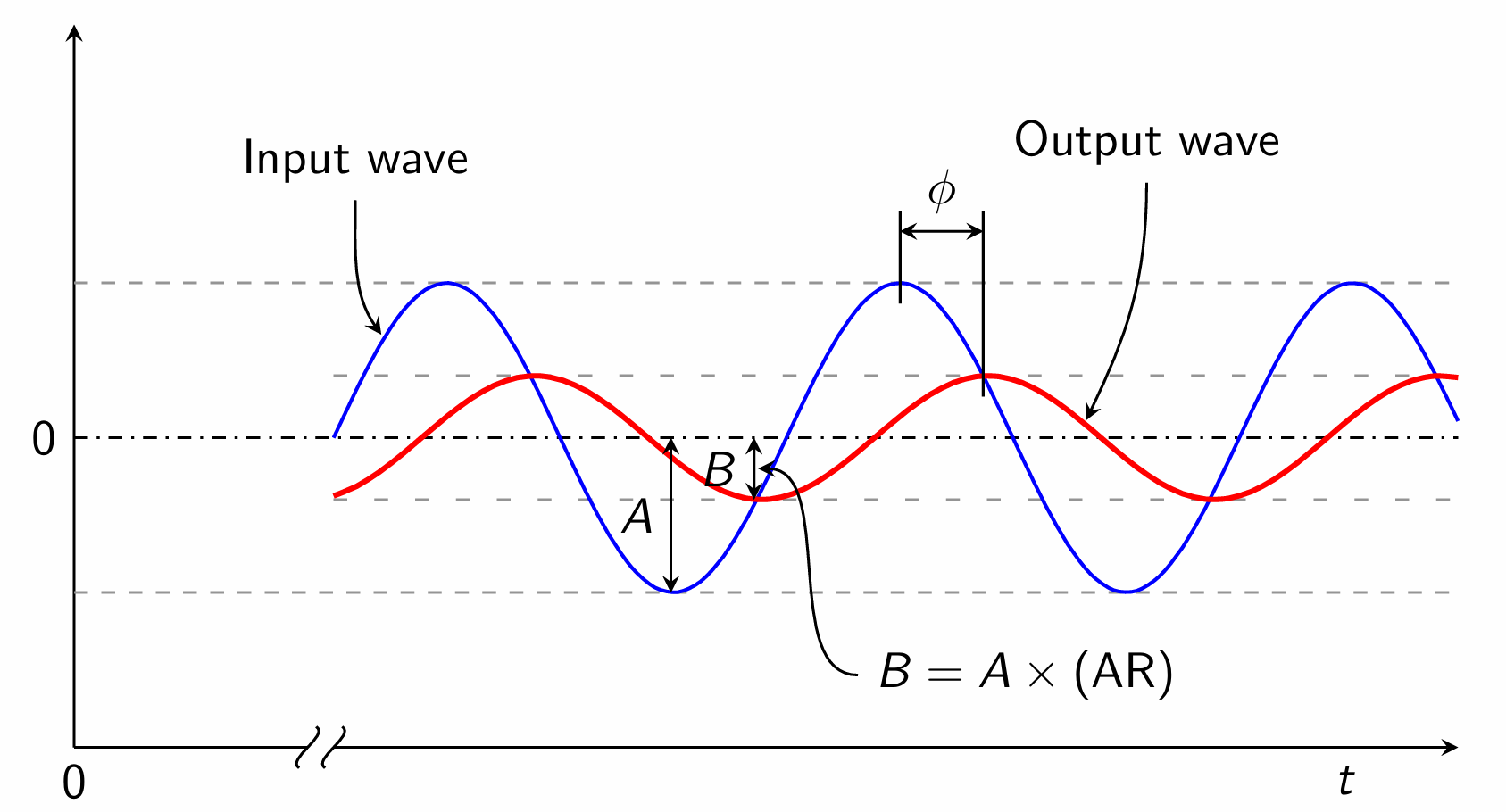
The ultimate response (also referred to as steady state) of a first order system to a sinusoidal input is also a sinusoidal wave with the same frequency \(\omega\).

The ration of output amplitude to input amplitude is called the amplitude ratio (AR) and is a function of frequency. \[\text{AR} = \frac{K_p}{\sqrt{\tau_p^2\omega^2+1}}\]

The output wave lags behind the input wave (phase lag) by an angle \(|\phi|\), which is also a function of \(\omega\).