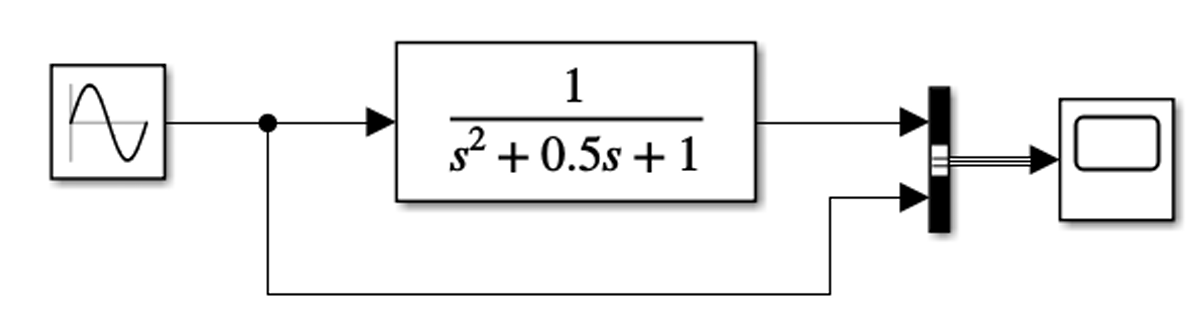11 - Frequency Response
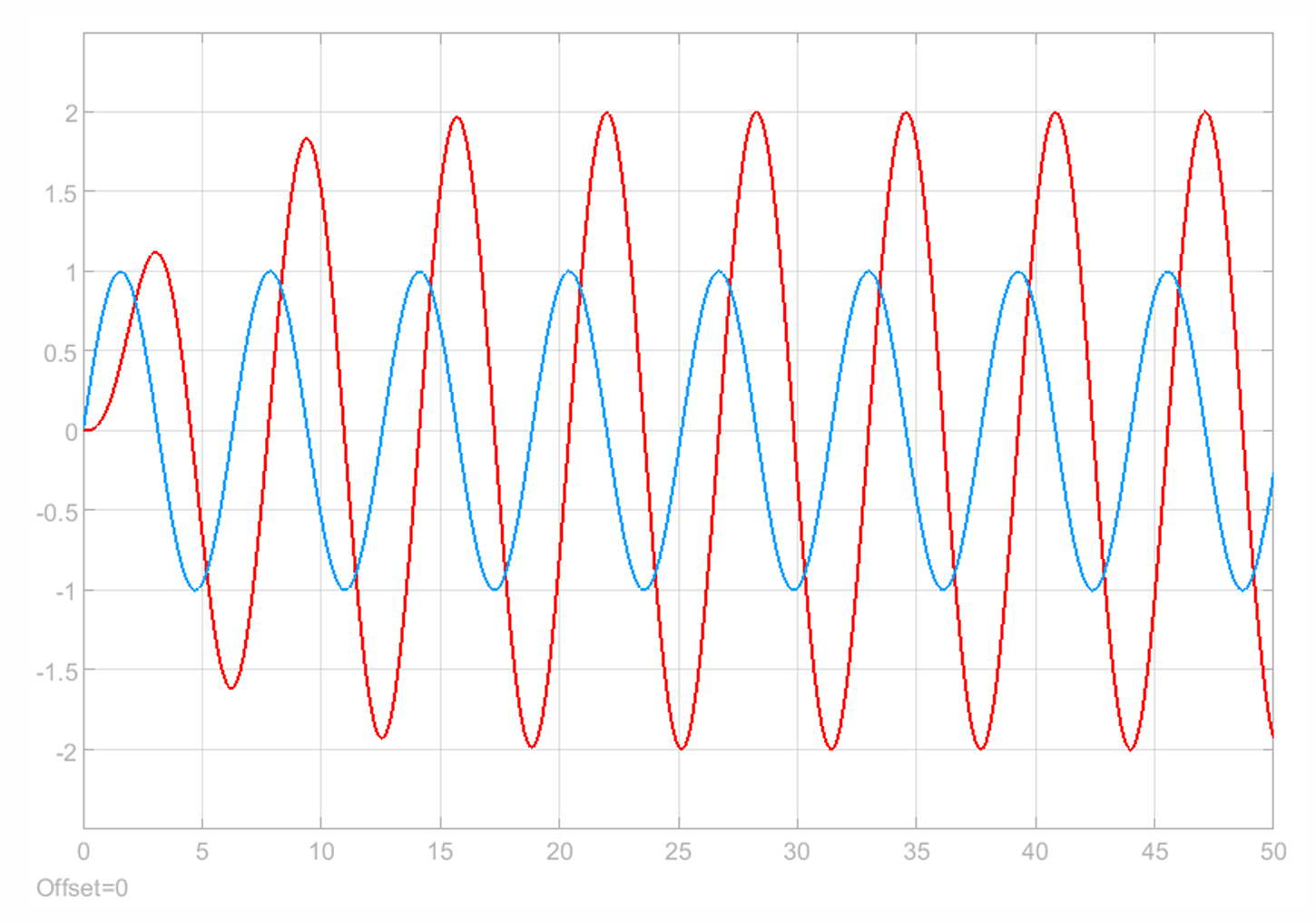
7. Frequency Response of Second Order System
For a second order system \[G(s) = \frac{K_p}{\tau^2s^2+2\zeta\tau s + 1}\] Put \(s=j\omega\) \[\begin{aligned} G(j\omega) &= \frac{K_p}{\tau^2(j\omega)^2+2\zeta\tau j\omega + 1} \\ &= \frac{K_p}{(-\tau^2\omega^2+1)+j2\zeta\tau\omega} \\ &= \frac{K_p}{(-\tau^2\omega^2+1)+j2\zeta\tau\omega}\frac{(-\tau^2\omega^2+1)-j2\zeta\tau\omega}{(-\tau^2\omega^2+1)-j2\zeta\tau\omega} \\ &= \frac{K_p(1-\tau^2\omega^2)}{(1-\tau^2\omega^2)^2+(2\zeta\tau\omega)^2}-j\frac{K_p\cdot2\zeta\tau\omega}{(1-\tau^2\omega^2)^2+(2\zeta\tau\omega)^2} \end{aligned}\]
Amplitude ratio: \[\text{AR} = |G(j\omega)| = \frac{K_p}{\sqrt{(1-\tau^2\omega^2)^2+(2\zeta\tau\omega)^2}}\] Phase shift: \[\phi = \text{argument of $G(j\omega)$} =\tan^{-1}\left(-\frac{2\zeta\tau\omega}{1-\tau^2\omega^2}\right)\] This is a phase lag since \(\phi<0\).