12. Bode Plots
Completion requirements
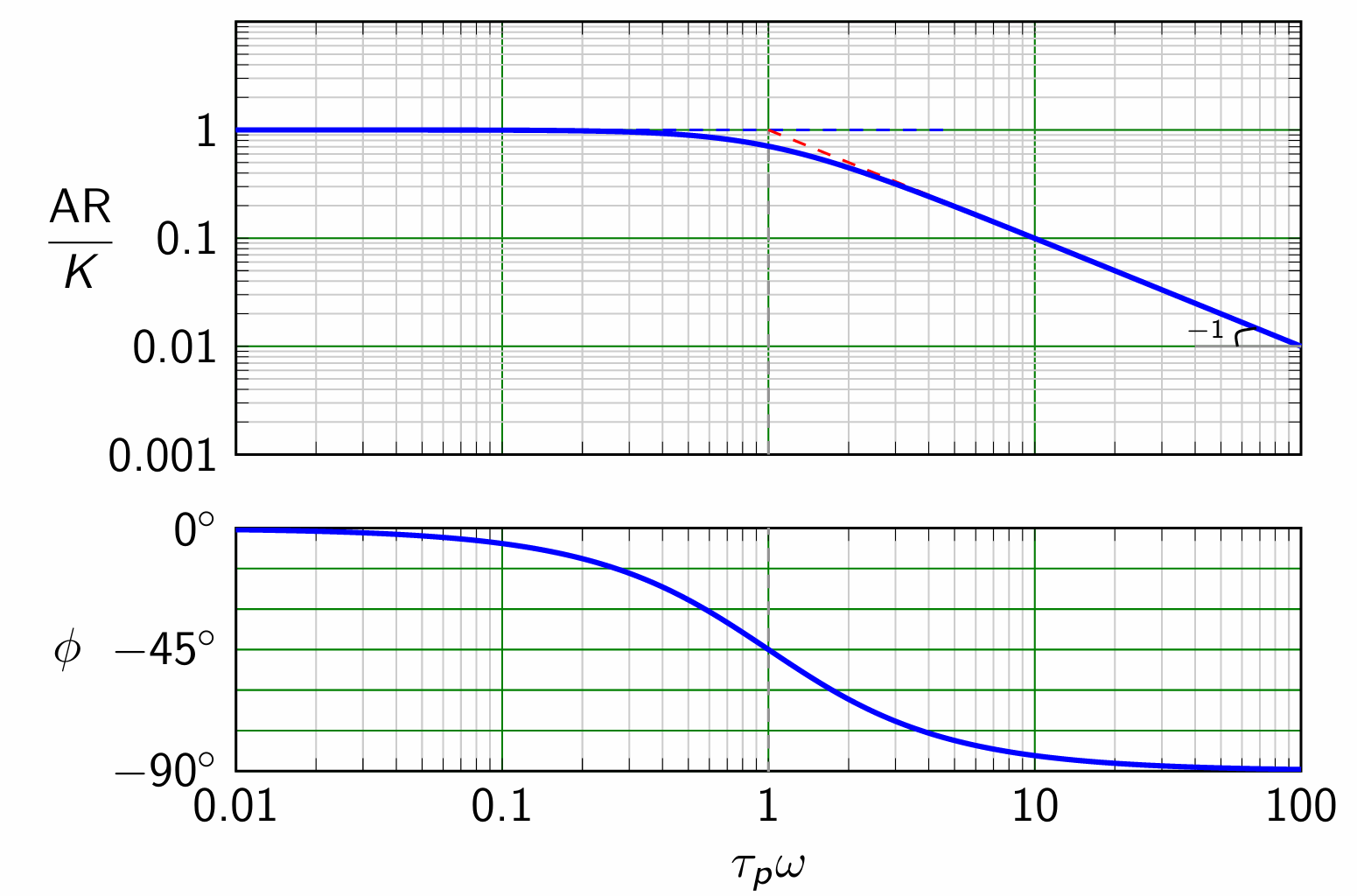
6. Bode Plots of First Order System
For first order system, \[\begin{aligned} \text{AR} &= \frac{K_p}{\sqrt{1+\tau_p^2\omega^2}} \\ \phi &= \tan^{-1}(-\tau_p\omega) \end{aligned}\] \[\log \left(\frac{\text{AR}}{K_p}\right) = -\frac{1}{2}\log(1+\tau_p^2\omega^2)\] The plot of \(\log(\text{AR}/K_p)\) versus \(\log(\tau_p\omega)\) is shown in figure (given in the following page) as a solid (blue) line.
Instead of the very elaborate numerical work needed to plot this graph, we can give an approximate sketch by considering its asymptotic behavior as \(\omega\rightarrow0\) and as \(\omega\rightarrow\infty\).