12. Bode Plots

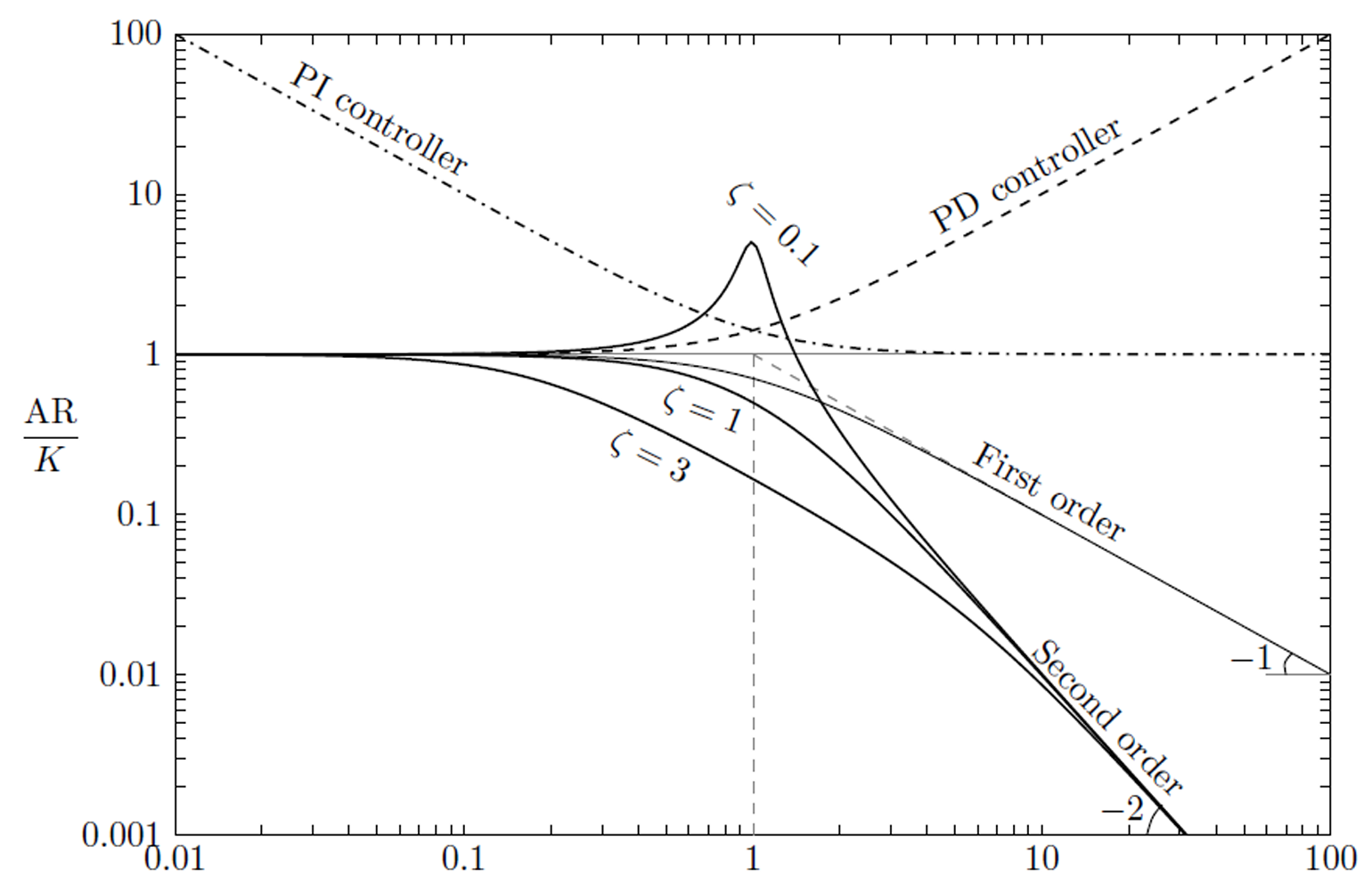
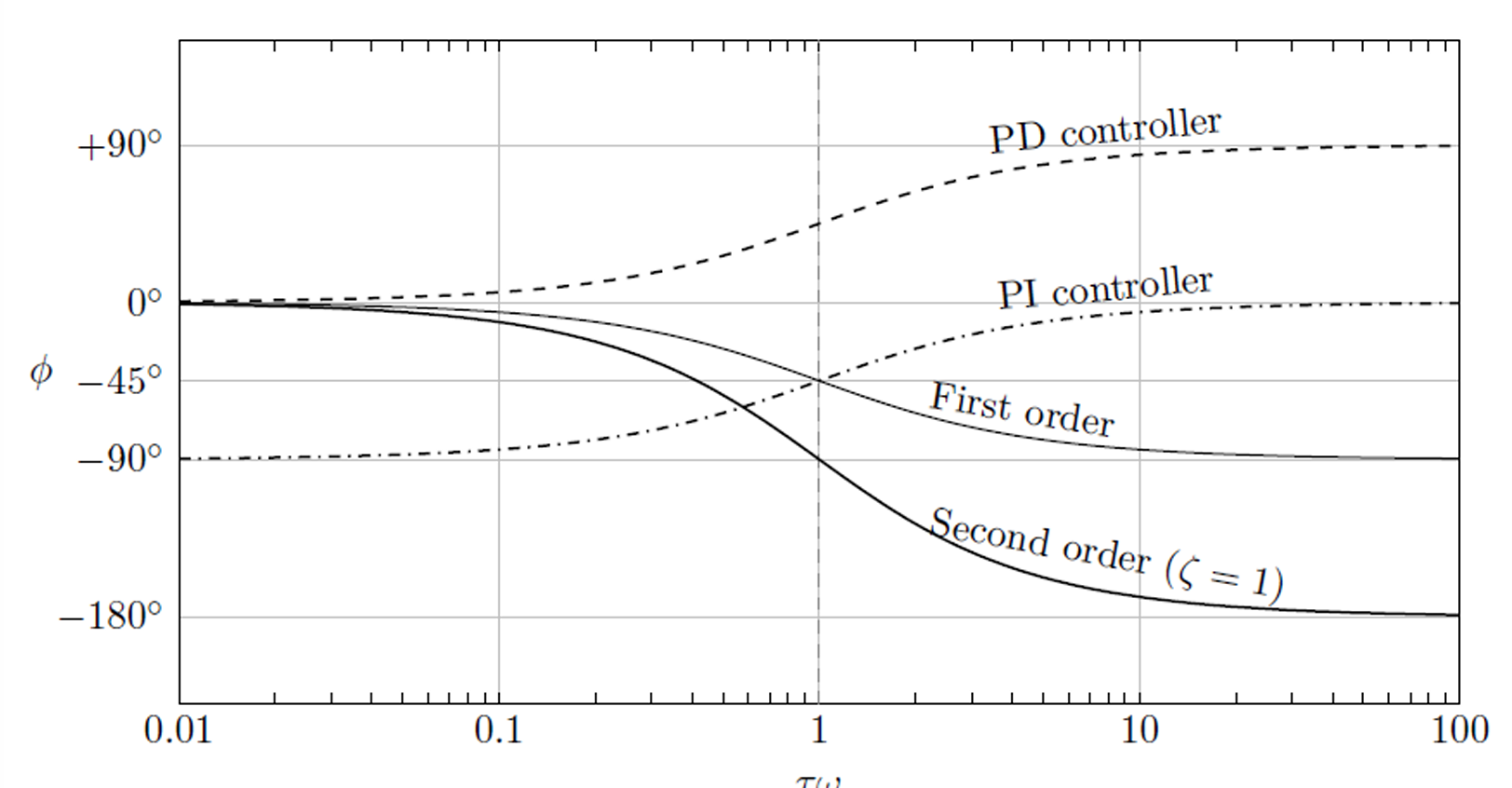
The overall transfer function is: \[G(s) = G_1(s)G_2(s)\cdots G_N(s)\] Overall phase shift \(\phi\): \[\phi = \phi_1 + \phi_2 + \cdots + \phi_N\] Overall amplitude ratio: \[\begin{aligned} \text{AR} &= (\text{AR})_1(\text{AR})_2\cdots(\text{AR})_N \\ \log(\text{AR}) &= \log(\text{AR})_1 + \log(\text{AR})_2+\cdots+\log(\text{AR})_N \end{aligned}\]

If the transfer function of a system can be factored into the product of \(N\) transfer functions of simpler systems, the following rules can be used for the construction of Bode plots:

The logarithm of the overall amplitude ratio is equal to the sum of the logarithms of the amplitude rations of the individual systems.

The overall phase shift is equal to the sum of the phase shifts of the individual systems.

The presence of a constant in the overall transfer function will move the entire AR curve vertically by a constant amount. It has no effect on the phase shift.