Maxwell Relations

\[\begin{align*} \left(\frac{\partial T}{\partial V}\right)_S &= -\left(\frac{\partial P}{\partial S}\right)_V \\ \left(\frac{\partial T}{\partial P}\right)_S &= \left(\frac{\partial V}{\partial S}\right)_P \\ \left(\frac{\partial P}{\partial T}\right)_V &= \left(\frac{\partial S}{\partial V}\right)_T \\ \left(\frac{\partial V}{\partial T}\right)_P &= -\left(\frac{\partial S}{\partial P}\right)_T \end{align*}\] These are obtained by applying the exactness criteria for each of the fundamental energy relations (viz, \(dU, dH, dA, dG\) respectively).

In the Maxwell relations, the two partial derivatives \(\displaystyle \left(\frac{\partial V}{\partial T}\right)_P\) and \(\displaystyle \left(\frac{\partial P}{\partial T}\right)_V\) are more useful, since they are readily obtainable from \(PVT\) properties.

  • Mnemonic Diagram: The fundamental property relations and Maxwell relations could be obtained from the mnemonic diagram as given in Fig.(8).

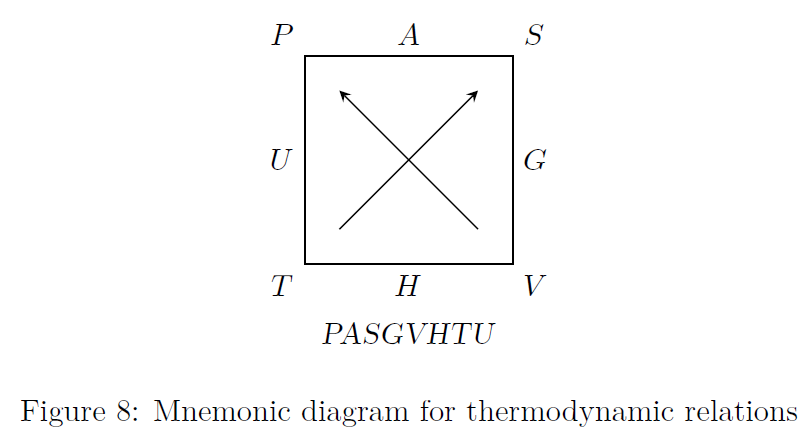
  • The fundamental energy properties are obtained as below:
    The variables available to the side (let us call as side variables) of the energy properties are written as such. The variables available at diagonally opposite corner (let us call as distant variables) are written as their corresponding differential variables, with proper sign convention:

    • if the arrow of  line (i.e., cross-lines) is pointing towards the side variable then, it is taken with negative sign.

    • if the arrow of line  is pointing away from the side variable then, it is taken with positive sign.

    For example for \(dU\), the side variables are \(P\) and \(T\). The distant variable corresponding to \(P\) is \(V\), and the corresponding arrow of  line is pointing towards (i.e., -ve). Similarly, the distant variable to \(T\) is \(S\) and the arrow of 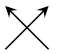line is pointing outwards (i.e., +ve). Therefore, we get \[dU = -PdV + TdS\]

  • The Maxwell relations are obtained from the mnemonic diagram as below:
    The variables (in the anti clockwise direction) on one side are connected with the variables exactly on the other side (in the clockwise direction), by a  line. The third variable in the same direction is taken as the constant. If the horizontal sides are equated, then, there is a negative sign.

    For example, the horizontal variables at the bottom of the mnemonic diagram are \(T\) and \(V\), (with \(S\) as constant) the variables on the corresponding opposite side are \(P\) and \(S\) (with \(V\) as constant). Since the connection is between two horizontal sides we will get a negative sign. \[\left(\frac{\partial T}{\partial V}\right)_S = -\left(\frac{\partial P}{\partial S}\right)_V\]

Cyclic Relation Rule

For the function in the variables \(x,y \ \& \ z\) \[\left(\frac{\partial x}{\partial y} \right)_z \left(\frac{\partial y}{\partial z} \right)_x \left(\frac{\partial z}{\partial x} \right)_y = -1\]

Other Relations of Importance

\[\left(\frac{\partial z}{\partial x} \right)_y = \left(\frac{\partial z}{\partial w} \right)_y \left(\frac{\partial w}{\partial x} \right)_y\] \[\left(\frac{\partial x}{\partial y} \right)_z = \dfrac{1}{\left(\frac{\partial y}{\partial x} \right)_z}\]

Tags: