Notes - Depreciation
Completion requirements
-
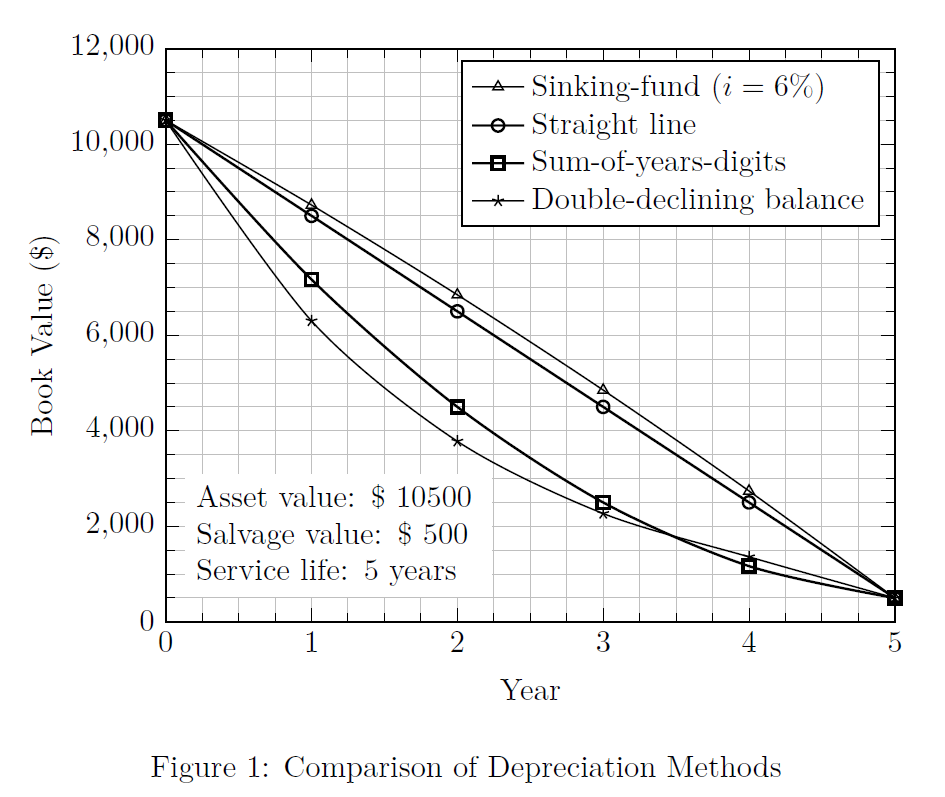
Comparison of Depreciation Methods: \[\text{Depreciation expense} = \text{Depreciation base} \times \text{Depreciation rate}\]
Method Depreciation base Depreciation rate Straight line \(V-V_s\) \(1/n\) Double declining balance \(V_i\) \(2/n\) Text-book declining balance \(V_i\) \(1-(V_s/V)^{1/n}\) Sum-of-years-digits \(V-V_s\) \(\dfrac{(n-a+1)}{\sum_1^n a }\) \(\qquad\qquad\) \(a\)–end of a particular year
\(V\) = asset value; \(V_s\) = salvage (or scrap) value; \(n\) = service life
\(V_i\) = value of asset at the start of the given yearVariation of book-value with time according to different methods of depreciation calculation is shown in Fig.(1). At any time, book-value is always higher with sinking-fund method. Book-value vs. time is constant for straight-line method. Declining-balance and sum-of-years-digits methods have low book-values at any time in comparison to straight-line method.