Notes - Open Loop Response
Higher Order Systems
Systems with order higher than one, can be represented by \[G(s) = \prod_{i=1}^n G_i(s) =\frac{K}{\prod_{i=1}^n(\tau_i s +1)}\]

Refer to Fig.(10) which illustrates the step response of an \(n\)-tank non-interacting system in series, for \(n = 2, 3, 4 \& 5\) in comparison with a single tank system. It can be approximated by a first order plus dead time system as \[G(s)=\frac{Ke^{-\tau_d s}}{\tau_1 s+1}\] where \(\tau_1\) is the dominant time constant, and, \[\tau_d= \sum_{i=2}^n\tau_i\] e.g.: \[G(s) = \frac{K}{(5s+1)(3s+1)(0.5s+1)} \approx \frac{K\,e^{-3.5s}}{5s+1}\] Here, \[\begin{aligned} \tau_1&=5 \quad (\text{the dominant time constant}) \\ \tau_d&=3+0.5=3.5 \quad (\text{the dead time}) \end{aligned}\]
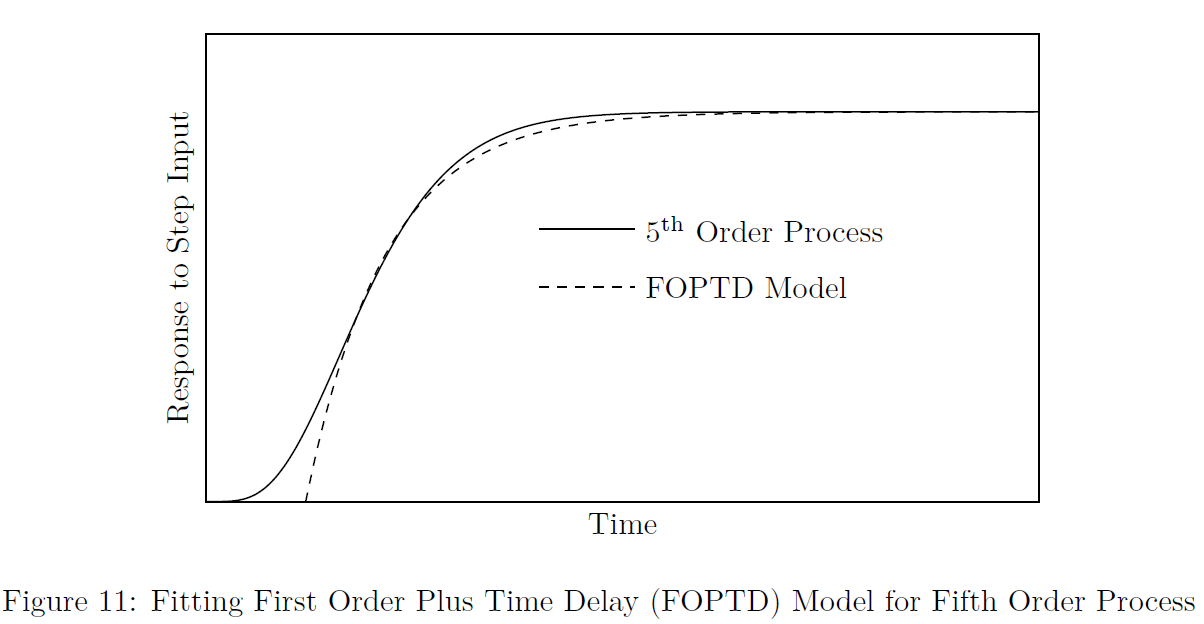
Refer to Fig.(11) which depicts the step response of a fifth order process which is fairly matched by a model called “First Order Plus Time Delay (FOPTD) model”.