2. Open Loop Response: Underdamped System

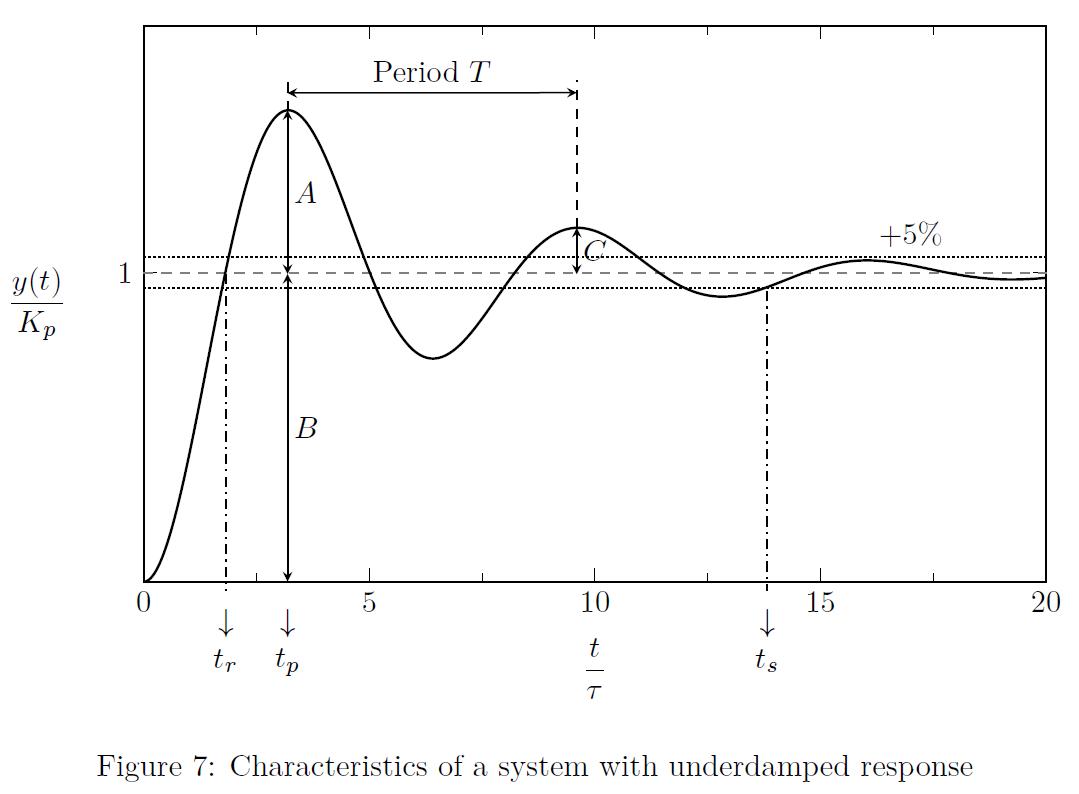
This is the most commonly exhibited behavior with second order systems. Refer to Fig.(7).

Rise time (\(t_r\)): It is the time the process output takes to first reach the new steady-state value.
Peak time (\(t_p\)): It is the time for the first peak to appear from the start of response. \[t_p = \frac{\pi \tau}{\sqrt{1-\zeta^2}}\]
Overshoot: It’s about how much the response exceeds its ultimate value. \[\text{Overshoot } = \frac{A}{B} = \exp\left(\frac{-\pi\zeta}{\sqrt{1-\zeta^2}}\right)\]
Decay ration: It’s the ratio of successive peaks of the response. \[\text{Decay ratio } = \frac{C}{A} = \text{(Overshoot)}^2 = \exp\left(\frac{-2\pi\zeta}{\sqrt{1-\zeta^2}}\right)\]
Period of oscillation (\(T\)). It is the time elapsed between two successive peaks (or two successive valleys) of the response. \[T = \frac{2\pi\tau}{\sqrt{1-\zeta^2}}\] and \[\omega = 2\pi f = \frac{2\pi}{T}\] Natural cyclical period of oscillation (\(T_n\)) is the period of oscillation at \(\zeta=0\). Hence, \[T_n = 2\pi\tau\]
Settling time (\(t_s\)): It is also known as response time. It is defined as the time required for the response to come within \(\pm5\%\) (or \(\pm2\%\)) of its ultimate value and remain there. It’s value is given as: \[t_s = \left\{\begin{array}{ll}\dfrac{4\tau}{\zeta} & (\text{2% criterion}) \\\\ \dfrac{3\tau}{\zeta} & (\text{5% criterion})\end{array} \right.\]

We note that it is often preferable that the transient response be sufficiently fast as well as reasonably damped. For a second order system, an optimal damping ratio \(\zeta\) is often chosen between 0.4 and 0.8. Too small \(\zeta\) always yields excessive overshoot in the transient response, while too large \(\zeta\) will make the response sluggish. Also, we observe that the maximum overshoot and the rise time conflict with each other. In other words, both the maximum overshoot and the rise time cannot be made smaller simultaneously. If one is made smaller, the other necessarily becomes larger.
If the fastest response time is desired, and a small overshoot can be tolerated, the damping ratio should be around 0.7 (optimally damped).