1. Introduction

(b) Method of Initial Rates (or) Initial Slopes

In this method, the concentrations of the reactants are monitored for a short interval of time, so that the changes in concentrations of reactants are not significant. Refer to Fig.(2).

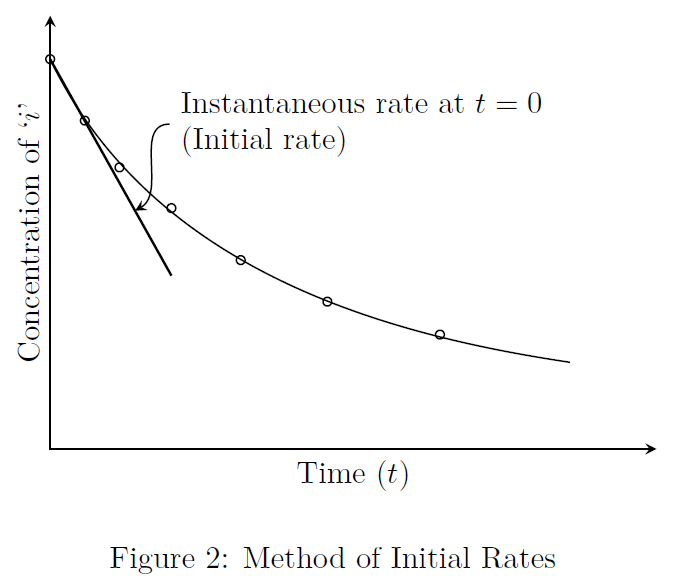
We know that, \[\text{rate} = \frac{d(\text{concentration})}{d(\text{time})}\] Consider the reaction between \(A\) and \(B\): \[A + 2B \rightarrow R\] Now, we shall conduct the reaction at two different initial concentrations of \(A\), keeping \(C_{B0}\) the same in both the runs. Similarly, we can perform the reaction at two different initial concentrations of \(B\), keeping \(C_{A0}\) constant in both the runs. The initial slopes of concentration versus time curves obtained give the initial reaction rates for the runs performed. Using this combined data, we can find the order of reaction with respect to each reactant and the value of the rate constant.

The method of initial rates / slopes is useful for slow reactions and reversible reactions, in the determination of the kinetic parameters.