2. Conduction
Heat Conduction with Multiple Resistances
The concept of thermal resistance (simply called as resistance here) is based on the observation that many diverse physical phenomena can be described by a general rate equation, stated as: \[\text{Flow rate} = \frac{\text{driving force}}{\text{resistance}}\]
The idea of thermal resistance is a useful tool for analyzing conduction through composite members, for steady state systems with no heat generation and constant thermal conductivities.
The idea of resistance was already introduced and discussed for conduction. By the same way, for convective heat transfer, resistance is given by, \[Q = hA(T_s-T_\infty) = \frac{(T_s-T_\infty)}{R} \qquad \text{where } R = \frac{1}{hA}\] And for radiation, \[\begin{aligned} Q &= \sigma \epsilon_1 A_1(T_1^4-T_2^4) = \sigma \epsilon_1 A_1(T_1^2+T_2^2)(T_1^2-T_2^2)= \sigma \epsilon_1 A_1(T_1^2+T_2^2)(T_1+T_2)(T_1-T_2) \\ &=\frac{(T_1-T_2)}{R} \end{aligned}\]
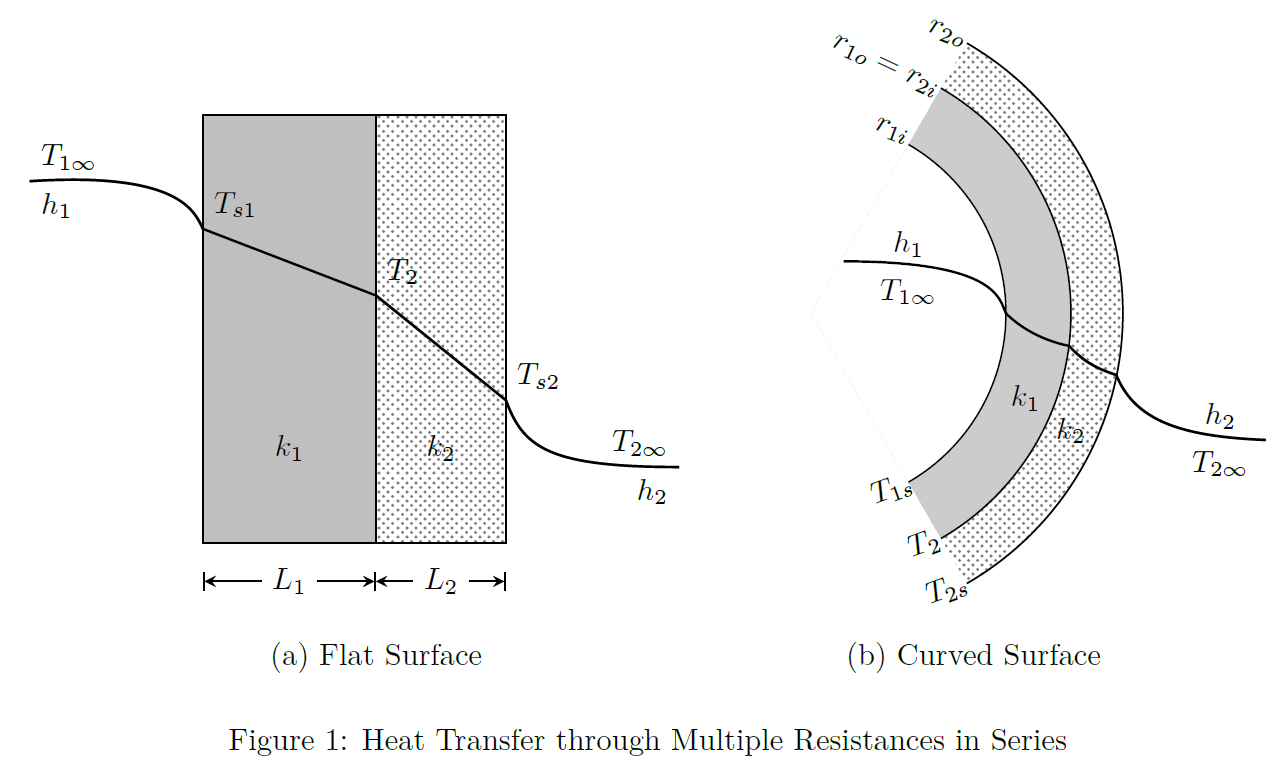
Composite Plane Wall
Refer to Fig.(1-a). \[\left(\begin{array}{c} \text{rate of heat} \\ \text{convection} \\ \text{into the wall 1} \end{array}\right) = \left( \begin{array}{c} \text{rate of heat} \\ \text{conduction} \\ \text{through wall 1} \end{array} \right) = \left( \begin{array}{c} \text{rate of heat} \\ \text{conduction} \\ \text{through wall 2} \end{array} \right) = \left( \begin{array}{c} \text{rate of heat} \\ \text{convection} \\ \text{from wall 2} \end{array} \right)\]
\[Q = \frac{T_{1\infty}-T_{1s}}{R_1} = \frac{T_{1s}-T_{2}}{R_2} = \frac{T_{2}-T_{2s}}{R_3} = \frac{T_{s2}-T_{2\infty}}{R_4}\] where \[R_1 = \frac{1}{h_1A} \qquad R_2 = \frac{L_1}{k_1A} \qquad R_3=\frac{L_2}{k_2A} \qquad R_4 = \frac{1}{h_2A}\] Adding the numerators and denominators separately, we get \[Q = \frac{T_{1\infty}-T_{2\infty}}{R_1+R_2+R_3+R_4}\]
Composite Curved Surfaces
Refer to Fig.(1-b). \[Q = \frac{T_{1\infty}-T_{2\infty}}{R_1+R_2+R_3+R_4}\] Cylindrical Surface: \[R_1 = \frac{1}{h_12\pi r_{1i}H} \qquad \ R_2 = \frac{\ln(r_{1o}/r_{1i})}{2\pi k_1H} \qquad \ R_3=\frac{\ln(r_{2o}/r_{2i})}{2\pi k_2H} \qquad \ R_4 = \frac{1}{h_2 2\pi r_{2o}H}\] Spherical Surface: \[R_1 = \frac{1}{h_14\pi r_{1i}^2} \qquad \ R_2 = \frac{(r_{1o}-r_{1i})}{4\pi k_1r_{1i}r_{1o}} \qquad \ R_3=\frac{(r_{2o}-r_{2i})}{4\pi k_2r_{2i}r_{2o}} \qquad \ R_4 = \frac{1}{h_24\pi r_{2o}^2}\]
