Instant Notes
-
For deviations from the ideal solution behavior, Raoult’s law can be used in the modified form as \[y_iP = \gamma_ix_iP_i^{\text{sat}} \tag*{(Modified Raoult's law)}\]
-
Deviations from Ideality \[\bar{P_i} = y_iP = \gamma_ix_iP_i^{\text{sat}} \quad\quad P= \sum{\bar{P_i}}\] where \(\bar{P_i} =\) partial pressure of component \(i\) in the vapor phase.
Deviations from ideality refer to systems with \(\gamma_i\ne1\). Deviations from ideality can be more (positive) or less (negative) as shown in Fig.(29).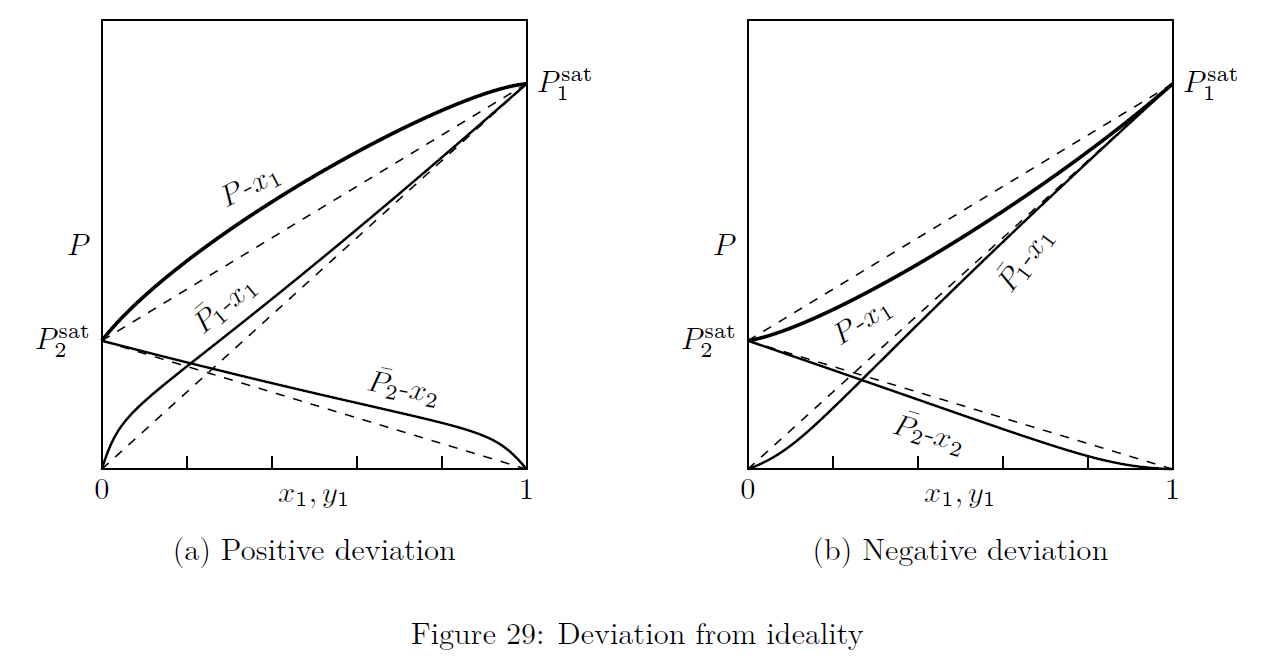
The dashed line represent the ideal solution behavior (\(\gamma_i=1\)). The deviations from ideality of either component is pronounced at very low concentrations of that component. The deviations get reduced, as the concentration of a component approaches 100%.-
Positive deviation from ideality: It is due to components with \(\gamma_i>1\). For such systems, \(\ln\gamma_i\) is positive, and hence the name positive deviation. Here, \(\bar{P_i} = y_iP = \gamma_ix_iP > x_iP_i^{\text{sat}}\)
-
Negative deviation from ideality: It is due to components with \(\gamma_i<1\). For such systems, \(\ln\gamma_i\) is negative, and hence the name negative deviation. Here, \(\bar{P_i} = y_iP = \gamma_ix_iP < x_iP_i^{\text{sat}}\)
-
