Instant Notes
Comparison between Raoult’s and Henry’s Laws
Henry’s law states that the partial pressure of component \(i\) in the vapor (or gas) phase (\(\bar{P_i}\)) is proportional to the its concentration in the liquid phase. i.e., \[\bar{P_i} = x_i H_i\] where \(x_i\) is the mole fraction of solute and \(H_i\) is known as the Henry’s law constant.
According to Raoult’s law, \[\bar{P_i} = x_iP_i^{\text{sat}}\] where \(x_i\) is the mole fraction of solvent and \(P_i^{\text{sat}}\) is the vapor pressure of the pure solvent.
Raoult’s and Henry’s laws are often termed as ‘limiting laws’. Raoult’s law is applicable at high concentrations of solute, and Henry’s law is applicable at low concentrations of solute. In other words Raoult’s law is applicable for the solvent, and Henry’s law for the solute. It is represented in Fig.(32).
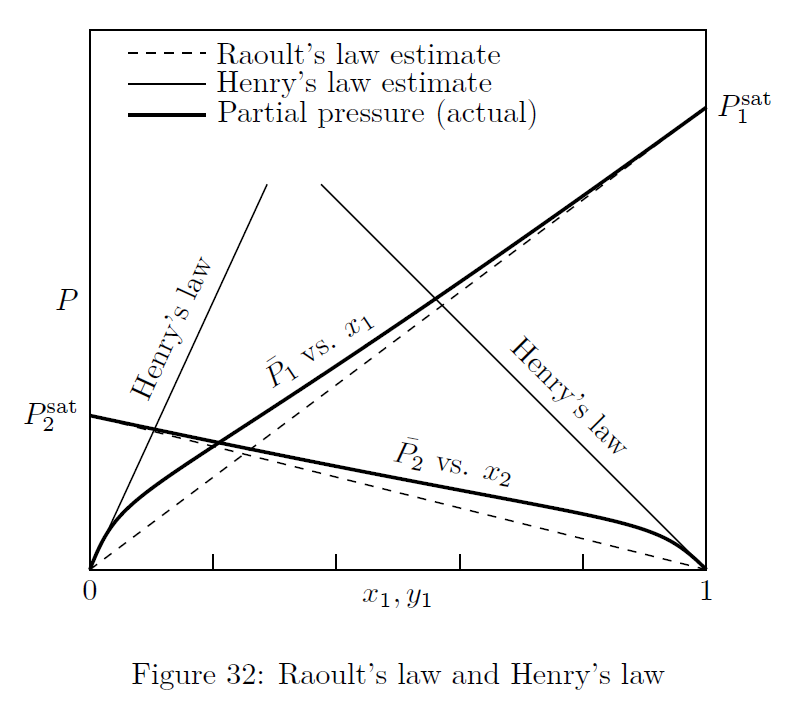
These two laws can be derived from the fundamental criterion of phase equilibrium, as below:
For the component \(i\) present in the coexisting vapor and liquid phases at equilibrium, \[\begin{align*}
\mu_i^V &= \mu_i^L \\
\text{i.e.,} \qquad \hat{f_i}^V &= \hat{f_i}^L \\
\text{Using $\phi-\gamma$ approach,} \\
\hat{\phi_i}y_iP &= \gamma_ix_iP_i^{\text{sat}} \\
\text{Considering the vapor as an ideal gas mixture, $\hat{\phi_i}=1$. Therefore,} \\
y_iP &= \gamma_ix_iP_i^{\text{sat}} \\
\text{i.e.,} \qquad \bar{P_i} &= \gamma_ix_iP_i^{\text{sat}} \\
\text{For component $i$ to be considered as a solvent, $x_i\rightarrow1$, and $\gamma_i=1$. Therefore,} \\
\bar{P_i} &= x_iP_i^{\text{sat}} \qquad \text{(Raoult's law)} \\
\text{For component $i$ to be considered as a solute, $x_i\rightarrow0$, and $\gamma_i=\gamma_i^\infty$. Therefore,} \\
\bar{P_i} &= x_i\gamma_i^\infty P_i^{\text{sat}} \\
\text{i.e.,} \qquad \bar{P_i} &= x_iH_i \end{align*}\]
The above is the Henry's law, where \( H_i=\text{ constant} = \gamma_i^\infty P_i^{\text{sat}} \)
