Conduction

Conduction is the transfer of energy due to either random molecular motion or due to the motion of ``free'' electrons.  


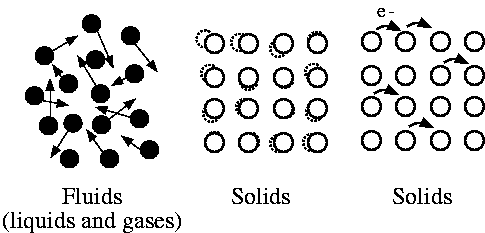
In different phases of matter, the modes of conduction are slightly different:

Gases: conduction is due to collisions of randomly moving molecules.

Liquids: similar to gases, but with a much smaller “mean free path”.

Solids: conduction is due to lattice vibrations and/or motion of "free" electrons.

In solid bodies, conduction is the significant heat transfer mechanism because no material flows in the process. With flowing fluids, conduction dominates in the region very close to the solid boundary, where the flow is laminar and parallel to the surface where there is no eddy motion.

Heat transfer rate and Heat flux:

\[ Q = qA \]

where

\(Q \) = heat transfer rate (J/s = W) 

\(q\) = heat flux (W/m2) 

\(A\) = heat transfer area (m2)


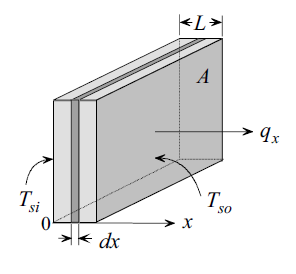
\[ \text{Rate of heat conduction} \propto \frac{\text{Area}\times\text{Temperature difference}}{\text{Thickness}} \]

\[ \boxed{Q = -kA\frac{dT}{dx}}\tag*{(Fourier's law)} \]

Fourier's law is a phenomenological law; that is developed from observed phenomena rather than being derived from first principles.

\[ Q = -kA\frac{dT}{dx} = kA\frac{\Delta T}{L} \]

where

\(\Delta T \) = \(T_{\text{in}}-T_{\text{out}}\)  (where  \(T_{\text{in}}>T_{\text{out}}\))

\(L\) = thickness of the wall

\(k\) = thermal conductivity of the material

  • Heat transfer rate in \(x\) direction is proportional to the temperature gradient, \(dT/dx\). The proportionality constant \(k\) is a transport property known as the thermal conductivity (W/m.K) and is a characteristic of the wall material.

  • The minus sign is a consequence of the fact that heat is transferred in the direction of decreasing temperature.

Central hole in the vadai (the snack item having urad dhal as ingredient) -- leads to increasing the area available for heat transfer. Increasing the surface area increases the rate of heat transfer, and hence faster cooking.