Instant Notes: 3. Gas-Liquid Contactors
Tray Efficiencies
-
Because a liquid changes in composition in passing across a tray, the tray efficiency of any type of cross flow tray increases somewhat with the diameter of the column, and efficiencies exceeding 100% have been observed in larger-diameter columns.
However, the tray efficiencies of distillation columns are in the range of 50–100%.
Murphree Tray Efficiency
Murphree tray efficiency is defined for each tray according to the separation achieved on each tray based on either the liquid phase or the vapor phase. The Murphree tray efficiency relates to the tray as a whole.
Murphree tray vapor efficiency (\(E_{MV}\)) is defined as the ratio of the actual change in a component vapor concentration as it flows through the tray to the change that would occur at equilibrium conditions. It is given as \[\begin{aligned} E_{MV} &=\frac{\text{composition of vapor leaving} - \text{composition of vapor entering}}{\binom{\text{composition of vapor leaving if it attained}}{\text{equilibrium with the leaving liquid}} - \text{ composition of vapor entering}} \\ &= \frac{y_{n}-y_{n-1}}{y_n^*-y_{n-1}} \end{aligned}\]
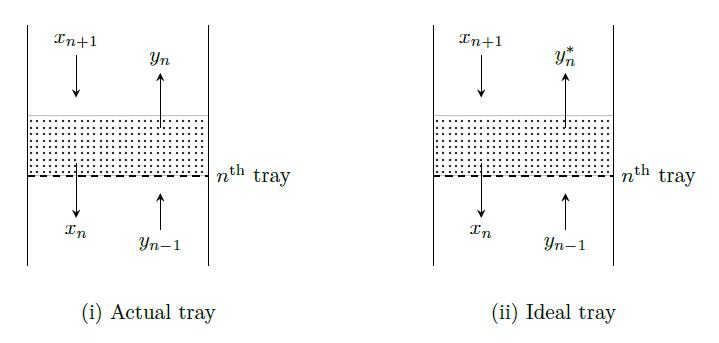
Tray \(n\), with a liquid composition \(x_n\), receives vapor with composition \(y_{n-1}\) from the tray below. If tray \(n\) were an equilibrium stage, the vapor leaving it would have a composition \(y_n^*\), determined by the equilibrium curve. The change in the vapor composition as it passes through tray \(n\) would be \(y_n^*-y_{n-1}\). In an actual tray, the vapor leaving tray \(n\) has a composition \(y_n\), resulting in a change in vapor composition of
\(y_n - y_{n-1}\). The value of \(y_n\) depends on the tray efficiency.
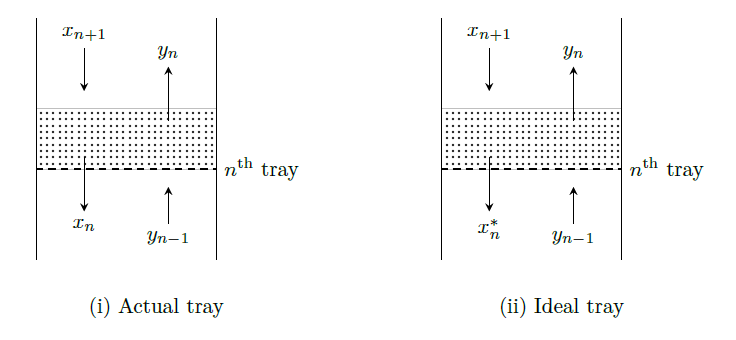
Murphree tray liquid efficiency (\(E_{ML}\)) is given as \[\begin{aligned}
E_{ML} &=\frac{\text{composition of liquid entering} - \text{composition of liquid leaving}}{\text{composition of liquid entering} - \binom{\text{composition of liquid leaving if it attained}}{\text{equilibrium with the leaving vapor}}} \\
&= \frac{x_{n+1}-x_n}{x_{n+1}-x_n^*} \end{aligned}\]
The Murphree tray efficiency is applicable under the assumption that the liquid phase and the vapor phase are completely mixed on each tray.
Since in general the liquid and vapor compositions vary along the length of the tray, a point efficiency is defined in terms of compositions at a given point on the tray. For example, in terms of vapor phase, point efficiency (\(E_V\)) is defined as \[E_V = \frac{y-y_{n-1}}{y^*-y_{n-1}}\] where \(y_{n-1}\) is the mole fraction of a given component in the mixed vapor coming from the tray below, designated as \(n-1\), and entering the tray in question, designated as \(n\). The actual mole fraction of the same component in the vapor at a given point on tray \(n\) is \(y\), and \(y^*\) is the vapor mole fraction of that component at equilibrium with \(x\), the mole fraction of the component in the liquid at the same point on tray \(n\).
Murphree point efficiency may be defined in terms of liquid compositions as well, as given below: \[E_L = \frac{x_{n+1}-x}{x_{n+1}-x^*}\] where \(x_{n+1}\) is an average mole fraction of a given component in the liquid flowing to tray \(n\) from the tray above, designated as \(n+1\). The actual mole fraction of the same component in the liquid at a given point on tray \(n\) is \(x\), and \(x^*\) is the mole fraction in the liquid of that component at equilibrium with \(y\), the vapor concentration at that point.
Note that the efficiency is defined for a particular component, implying that different components could have different efficiencies. This reflects the different rates of mass transfer for each component.
-
Murphree efficiency is the efficiency determined for a single tray.
-
In small diameter columns, the liquid on a plate is sufficiently agitated by vapor flow through the perforations for there to be no measurable concentration gradients in the liquid as it flows across the plate. Since the concentration of the liquid on the plate is constant, that of the vapor from the plate is also constant and no gradients exist in the vapor streams across the cross-section. So for small diameter columns, the local (point) and Murphree efficiencies are equal.
-
In larger columns, liquid mixing in the direction of flow is not complete, and a concentration gradient does exist in the liquid on the plate. For these conditions the local efficiency is considerably lower than the Murphree efficiency.
Murphree efficiency can exceed 100%, but the local efficiency can not be greater than 100%.
