2. Conduction
2.1 One Dimensional Heat Conduction Equation
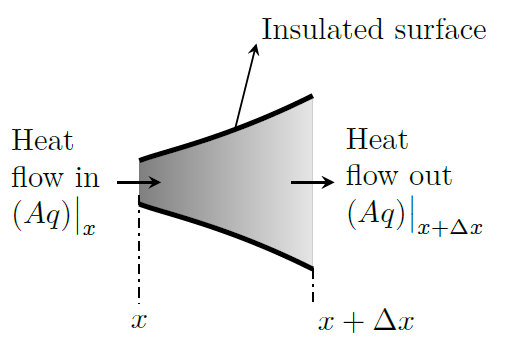
Let us consider a volume element of thickness \(\Delta x\) and having an area \(A\) normal to the coordinate axis \(x\), as shown in the figure. The energy balance equation for this volume element is given by: \[{\left(\begin{array}{c}\text{Net rate of} \\ \text{heat gain by} \\ \text{conduction} \end{array}\right)} + {\left(\begin{array}{c}\text{rate of} \\ \text{energy} \\ \text{generation} \end{array}\right)} = {\left(\begin{array}{c}\text{rate of} \\ \text{increase of} \\ \text{internal energy} \end{array}\right)} \tag*{(5)}\] The net rate of heat gain by the element by conduction is given by \[\text{I} = (Aq)\big|_{x} - (Aq)\big|_{x+\Delta x}\]
The rate of energy generation in the element having a volume \(A\Delta x\) is given by \[\text{II} = A\Delta x \dot{g}\] where \(\dot{g}=\dot{g}(x,t)\) is the rate of energy generation per unit volume; \(t\) is time.
The rate of increase of internal energy of the volume element resulting from the change of temperature is given by \[\text{III} = A\Delta x \,\rho C_P\frac{\partial T(x,t)}{\partial t}\] (Note: Internal energy change is \(mC_V\Delta T\); but for liquids and solids, \(C_P\approx C_V\)).
Substituting for the quantities in Eqn.(5), and rearranging, we get \[-\frac{1}{A}\frac{\left((Aq)\big|_{x+\Delta x} - (Aq)\big|_{x}\right)}{\Delta x} + \dot{g} = \rho C_P\frac{\partial T(x,t)}{\partial t} \tag*{(6)}\] As \(\Delta x \rightarrow 0\), \[\frac{\left((Aq)\big|_{x+\Delta x} - (Aq)\big|_{x}\right)}{\Delta x} = \frac{\partial}{\partial x}(Aq) \qquad (\text{from the definition of derivative})\] And from Fourier’s law: \(\displaystyle q=-k\frac{\partial T}{\partial x}\). Hence, Eqn.(6) becomes, \[\frac{1}{A} \frac{\partial}{\partial x}\left(Ak\frac{\partial T}{\partial x}\right) + \dot{g} = \rho C_P\frac{\partial T(x,t)}{\partial t} \tag*{(7)}\] This is the general equation for one dimensional heat conduction.
-
Rectangular Coordinates:
Here, the area \(A\) does not vary with \(x\). Hence, Eqn.(7) becomes, \[\frac{\partial}{\partial x}\left(k\frac{\partial T}{\partial x}\right) + \dot{g} = \rho C_P\frac{\partial T(x,t)}{\partial t}\]
-
Cylindrical Coordinates:
Here, \(x=r\), the radius of cylinder; and area, \(A=2\pi rH\), where \(H\) is height of the cylinder. For heat transfer in the radial direction, \(A\propto r\). Hence, Eqn.(7) becomes, \[\frac{1}{r}\frac{\partial}{\partial r}\left(rk\frac{\partial T}{\partial r}\right) + \dot{g} = \rho C_P\frac{\partial T(r,t)}{\partial t}\]
-
Spherical Coordinates:
Here too, \(x=r\). Area, \(A=4\pi r^2\). i.e., \(A\propto r^2\). Hence, Eqn.(7) becomes, \[\frac{1}{r^2}\frac{\partial}{\partial r}\left(r^2k\frac{\partial T}{\partial r}\right) + \dot{g} = \rho C_P\frac{\partial T(r,t)}{\partial t}\]
-
Compact Equation:
The above equations (rectangular / cylindrical / spherical coordinates) can be written in a compact form, as below: \[\frac{1}{r^n} \frac{\partial}{\partial r}\left(r^nk\frac{\partial T}{\partial r}\right) + \dot{g} = \rho C_P\frac{\partial T}{\partial t} \tag*{(8)}\] where \[n = \left\{\begin{array}{ll} 0 & \text{for rectangular coordinates} \\ 1 & \text{for cylindrical coordinates} \\ 2 & \text{for spherical coordinates} \end{array} \right.\] In the rectangular coordinates, it is customary to use the variable \(x\) in place of \(r\).
-
Special Cases:
-
For constant thermal conductivity \(k\), Eqn.(8) reduces to, \[\frac{1}{r^n} \frac{\partial}{\partial r}\left(r^n\frac{\partial T}{\partial r}\right) + \frac{1}{k}\dot{g} = \frac{1}{\alpha}\frac{\partial T}{\partial t}\] where \[\alpha = \frac{k}{\rho C_P} = \text{thermal diffusivity of material, m$^2$/s}\]
-
For steady state heat conduction with energy sources within the medium, Eqn.(8) reduces to, \[\frac{1}{r^n} \frac{d}{d r}\left(r^nk\frac{d T}{d r}\right) + \dot{g} = 0\] and for the case of conduction with constant \(k\), \[\frac{1}{r^n} \frac{d}{d r}\left(r^n\frac{d T}{d r}\right) + \frac{1}{k}\dot{g} = 0\]
-
For steady state conduction, with no energy sources, and for constant \(k\), \[\frac{d}{d r}\left(r^n\frac{d T}{d r}\right) = 0\]
-
-
During steady one-dimensional heat conduction the rate of heat transfer (\(Q\)) remains constant, but the heat flux (\(q\)) changes according to the heat transfer area (\(A\)).
-
For flat surfaces, \(A\) is constant in the direction of flow. Hence, the heat transfer flux (\(q=Q/A\)) is also constant. For curved surfaces, heat transfer area (\(A\)) varies along the direction of flow. For example, for flow through concentric cylinder heat transfer area increases with increase in radius. Hence heat flux (\(Q/A\)) decreases with increase in radius.
