Instant Notes: 2. Interpretation of Batch Reactor Data
(b) Irreversible Bimolecular-type Second-order Reactions
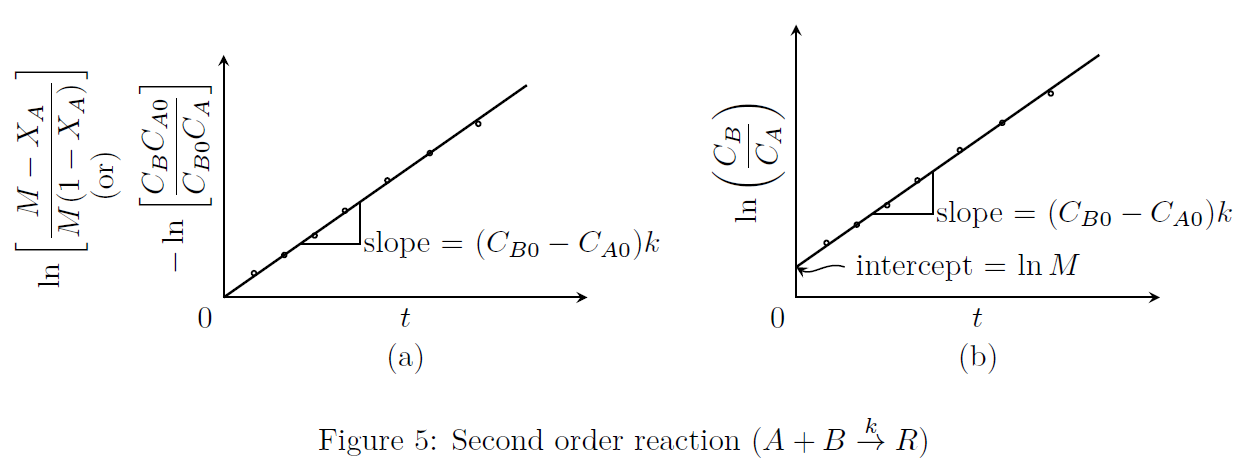
\[A + B \stackrel{k}{\rightarrow} R\] \[-r_A = kC_AC_B = -\frac{dC_A}{dt} = -\frac{dC_B}{dt}\] Let \[M = \frac{C_{B0}}{C_{A0}}\] Case-1 ( \(C_{A0}\ne C_{B0}\)): \[\begin{align*} -r_A &= -\frac{dC_A}{dt} =kC_{A0}(1-X_A)(C_{B0}-C_{B0}X_B) \nonumber \\ \text{where $C_{B0}X_B$ is the amount of `$B$' consumed.} \\ \text{From the stoichiometry, $C_{A0}X_A=C_{B0}X_B$. Hence,} \\ -r_A &= kC_{A0}(1-X_A)(MC_{A0}-C_{A0}X_A) \nonumber \\ -r_A &= kC_{A0}^2(1-X_A)(M-X_A) \tag*{(4)}\end{align*}\] Upon further reduction, we get \[\begin{multline*} \ln\left(\frac{1-X_B}{1-X_A}\right) = \ln\left(\frac{M-X_A}{M(1-X_A)}\right) = \ln\left(\frac{C_BC_{A0}}{C_{B0}C_A}\right) = \ln\left(\frac{C_B}{MC_A}\right) = \ldots \\ \ldots = C_{A0}(M-1)kt = (C_{B0}-C_{A0})kt \qquad (\text{for $M\ne1$}) \tag*{(5)}\end{multline*}\] Eqn.(5) is represented in Fig.(5).
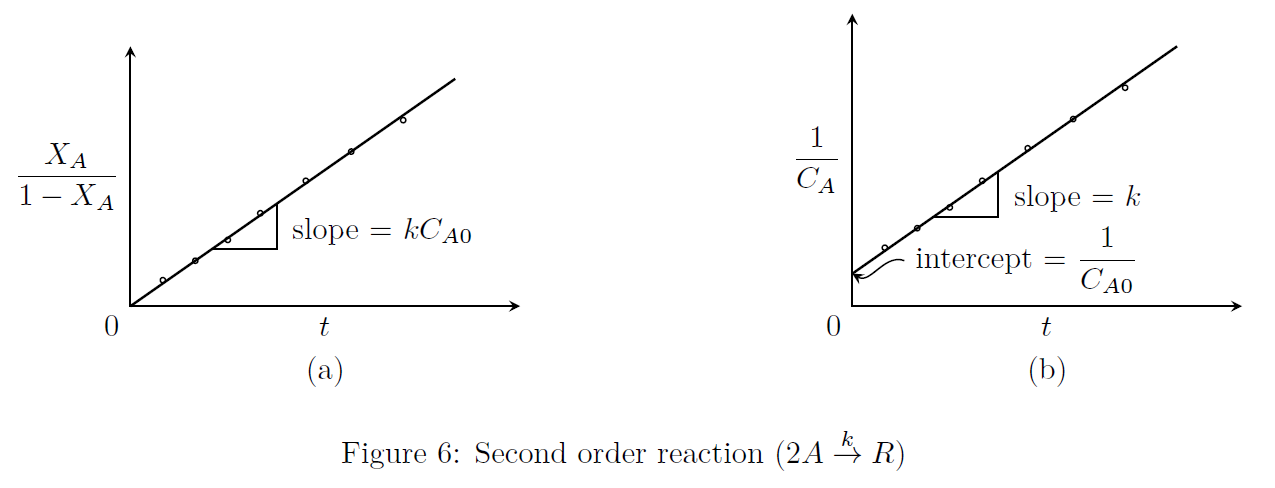
Case-2 (\(C_{A0}=C_{B0}\)): Then, Eqn.(4) becomes, \[\begin{align*}
-r_A &= kC_{A0}^2(1-X_A)^2 \nonumber \\
&= kC_A^2 \qquad [\because \quad C_A=C_{A0}(1-X_A)] \tag*{(6)}\\
\text{Upon further reduction, we get} \\
\frac{1}{C_A}-\frac{1}{C_{A0}} &= kt \tag*{(7)} \\
\frac{X_A}{1-X_A} &= kC_{A0}t \tag*{(8)}\end{align*}\] Eqns.(7, 8) are represented in Fig.(6).