1.1 Stress-Strain Relationship of Engineering Materials

Refer to Fig.(1).


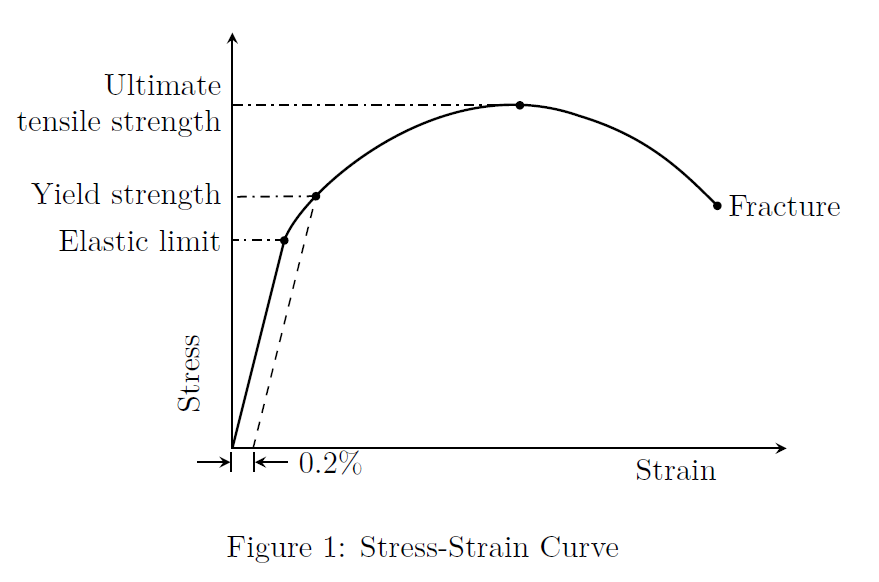
  • The degree to which a structure deforms or strains depends on the magnitude of an imposed stress. For most metals that are stressed in tension and at relatively low levels, there is a linear relationship between stress and strain (obeying Hooke’s law), till the elastic limit. \[\text{Strain} \propto \text{Stress} \tag{Hooke's law}\]

  • Elastic limit is the limiting value of stress up to which the material is perfectly elastic which means that when the applied load is released, the piece returns to its original shape. Stress-strain curve is linear up to this limit. Slope of this linear curve is called as Young’s modulus or modulus of elasticity.

  • Most structures are designed to ensure that only elastic deformation will result when a stress is applied. Elastic deformations are assumed to occur till the yield strength. Yield strength is obtained by the intersection of stress-strain curve (if it is smooth) with a straight line constructed parallel to the elastic portion of the stress-strain curve at some specified strain offset, usually 0.2%.

    For those materials having a non-smooth stress-strain curve, use of the strain offset method is not possible, and the usual practice is to define the yield strength as the stress required to produce some amount of strain (e.g., 0.5%).

    The magnitude of the yield strength for a metal is a measure of its resistance to plastic deformation.Yield strengths may range from 35 MPa for a low-strength aluminum to over 1400 MPa for high-strength steels.

  • After yielding, the stress necessary to continue plastic deformation in metals increases to a maximum, and then decreases to the eventual fracture. The tensile strength (or called as, Ultimate tensile strength) is the stress at the maximum on the stress-strain curve. This corresponds to the maximum stress that can be sustained by a structure in tension; if this stress is applied and maintained, fracture will result.