51 - Heat Exchangers - LMTD Method

\[Q = \frac{\Delta T}{R} = UA\Delta T = U_iA_i\Delta T = U_oA_o\Delta T\]

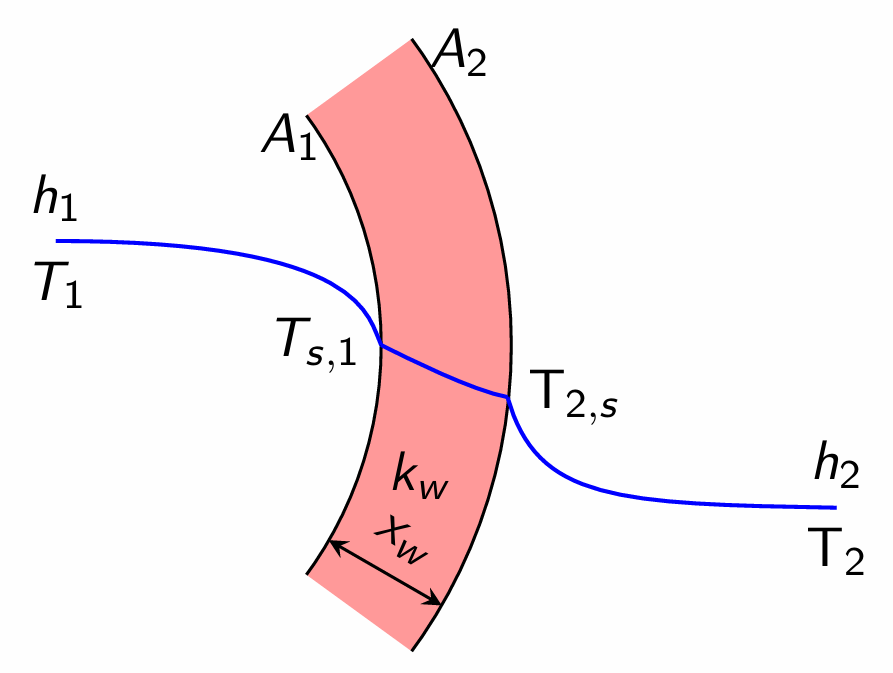
\[T_1 - T_{1,s} = \frac{Q}{h_1A_1} \qquad T_{1,s}-T_{2,s} = \frac{x_wQ}{k_wA_m} \qquad T_{2,s}-T_2= \frac{Q}{h_2A_2}\] Adding the numerator and denominator separately, we get \[T_1-T_2= \Delta T = Q\left[\frac{1}{h_1A_1} + \frac{x_w}{k_wA_m} + \frac{1}{h_2A_2} \right]\] From the relation \(Q=U_1A_1\Delta T\), we get \[\frac{Q}{U_1A_1} = Q\left[\frac{1}{h_1A_1} + \frac{x_w}{k_wA_m} + \frac{1}{h_2A_2} \right]\] i.e., \[\frac{1}{U_1} = \frac{1}{h_1} + \frac{x_w}{k_w}\frac{A_1}{A_m} + \frac{1}{h_2}\frac{A_1}{A_2}\] Similarly, we can also write \[\frac{1}{U_2} = \frac{1}{h_2} + \frac{x_w}{k_w}\frac{A_2}{A_m} + \frac{1}{h_1}\frac{A_2}{A_1}\]

For thin-walled tubes, where \(A_1\approx A_2\approx A_m\), we can write, \[\frac{1}{U} = \frac{1}{h_1} + \frac{x_w}{k_w} + \frac{1}{h_2}\] For the case of highly conducting wall, we can write the above as, \[\frac{1}{U} = \frac{1}{h_1} + \frac{1}{h_2}\]