Instant Notes
-
Internal Energy
Internal energy (\(U\)) is the energy due to molecular, atomic, and subatomic motions and interactions. It is the sum of the total kinetic energy and the total potential energy of all the atoms or molecules in the system that is at rest as a whole. Note that the internal energy does not include the kinetic energy due to the motion of the system as a whole nor the potential energy of the system as a whole due to an external field.Internal energy can not be measured directly, but the change of which (i.e., \(\Delta U\)) during a process, can be calculated by measuring the temperature change of the system.
Statement of First Law of Thermodynamics
It’s the law of conservation of energy. In thermodynamics, it is restated as: Change in total energy of the system is compensated by an equal and opposite change in the total energy of the surroundings. In mathematical terms, it is given as \[\Delta U + \Delta E_k + \Delta E_p = Q+W\] where \(\Delta U\) is the change in internal energy of the system; \(\Delta E_k\) is the change in kinetic energy of the system; \(\Delta E_p\) is the change in potential energy of the system; and, \(Q\) and \(W\) are heat and work interactions between the system and surrounding.
-
In many applications of the first law, the system undergoes no change in external potential or kinetic energy, but only changes in internal energy. Under these conditions, the first law becomes: \[\Delta U = Q + W \tag*{(11)}\]
-
Sign Conventions for Heat and Work
There are two sign conventions in common use, as represented in Fig.(7).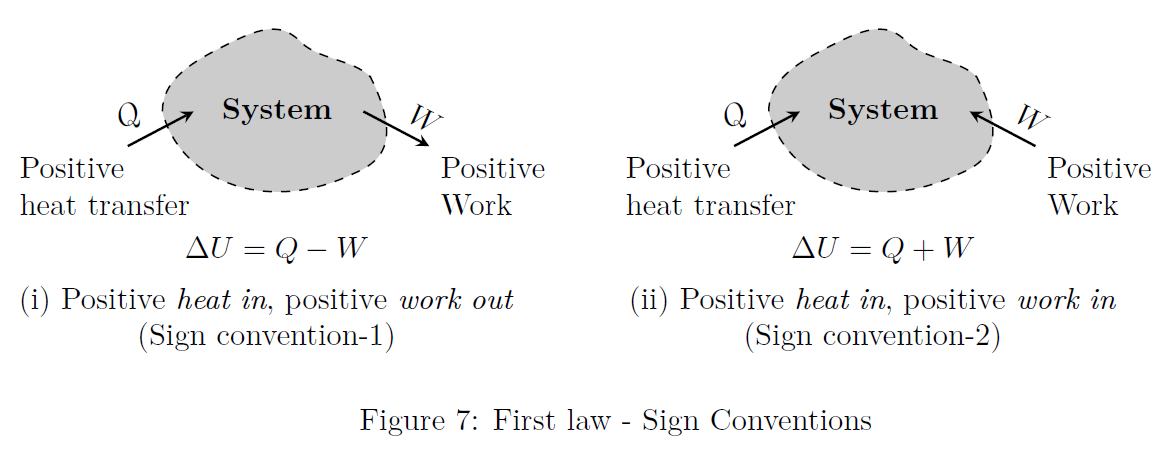
According to the first convention, \[\Delta U = Q - W\] Here, \(W=\int PdV\). i.e., work done by the system is positive.According to the second convention (In this book this second convention is used), \[\Delta U = Q + W\] Here, \(W=-\int PdV\). i.e., work done on the system is positive.
-
Enthalpy
Enthalpy, denoted as \(H\), is defined as below: \[H = U + PV \tag*{(12)}\] The quantity \(PV\) is called as flow energy; the significance of which will be introduced shortly.
